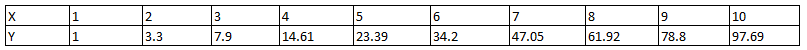Updated July 5, 2023
Introduction to Anonymous Function in Matlab
In Matlab, there are various inbuilt functions (multiple libraries are available in Matlab ). These inbuilt functions make Matlab easy and more powerful. But if we want to create our own function, then there is one option in Matlab, which is a function handle. By using a function handler, we can create any mathematical function; these functions are called anonymous functions.
Let us consider one example, y = – 2; in this, there are two variables, x, and y. x is input, and y is output. The value of y depends on the value of x.
So anonymous function representation will be y = @ ( x ) ^ 3 – 2
In the above equation, y is the function handler, x is the input variable, and ‘@ ‘is a symbol used for an anonymous function.
After writing this equation, we can give any value of x . for example, y ( 0 ), y ( 1 ), y ( 2 ), y ( 3 ), etc
If value of x is 0 then y = x ^ 3 – 2
Y = 0 – 2
Y = – 2
Similarly, if the value of x is 1 then y = 1 ^ 3 – 2
Y = 1 – 2
Y = -1
Steps to Write Anonymous Function in Matlab
Here we have discussed the steps to write a function in Matlab.
Step 1: First, define the Matlab handle function by using the ‘@ ‘symbol and input variable, y = @ ( x )
Step 2: Write the whole equation next to the function handler variable.
Step 3: Accept the input value inside the output variable, y ( 0).
Syntax:
Function definition;
Body of function;
Let us consider one equation p = q ^ 2 – 3
| Matlab Code | Syntax |
| P = @ ( q ) | Function handle variable = @ input variable |
| q ^ 2 – 3 | Mathematical equation |
| q ( 1 ) | Function handle variable( input variable value) |
Examples of Anonymous Functions in Matlab
Below are the different examples of anonymous functions in matlab as follows:
Example #1
Y = x3 + 2x
In this example, we will see a simple method of anonymous function.
Here, Y is the output, x is the variable input,
If we put x = 0
Y = 0 + 2 ( 0 )
Y = 0
If we put x = 1
Y = x3 + 2x
Y = 1 + 2
Y = 3
If we put x = 2
Y = x3 + 2x
Y = 8 + 4
Y = 12
If we put x = 3
Y = x3 + 2x
Y = 27 + 6
Y = 33
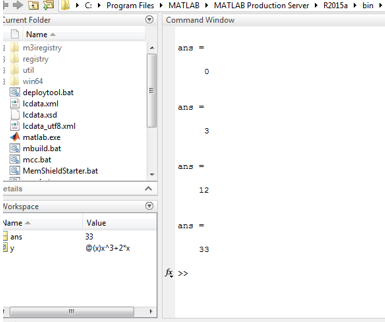
Matlab Code:
clc ;
y = @ ( x ) x. ^ 3 + (2 * x) ;
y ( 0 )
y ( 1 )
y ( 2 )
y ( 3 )
In the above code, y takes values of x at compile time. Screen 1 shows the implementation of example 1 in Matlab
Example #2
y = x3 – 2*x + 3
if x = 1
y = 1 – 2 + 3
y = 2
if x = 2
y = 8 – 4 + 3
y = 7
if x = 3
y = x3 – 2*x + 3
y = 27 – 6 + 3
y = 24
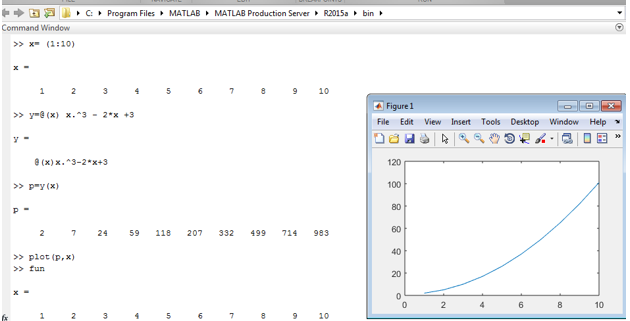
Matlab Code:
X = ( 1 : 10 )
y = @ ( x ) x . ^ 3 – 2 * x + 3
p = y ( x )
plot (y, x )
In the above code, x ranges from 0 to 10, so there is no need to assign values of ‘x at the time of compilation, and if discrete values of x and y are known, then we can plot the response of variables x and y. Screen 2 shows the implementation of Example 2 and the response of x and y.
Example #3
Y = x2 – log(x)
In this example, it isn’t easy to find a logarithm for each value of x; instead of mathematical calculations, if we use direct Matlab commands, we will get output with all values of y and the response of x vs y (by using plot command).
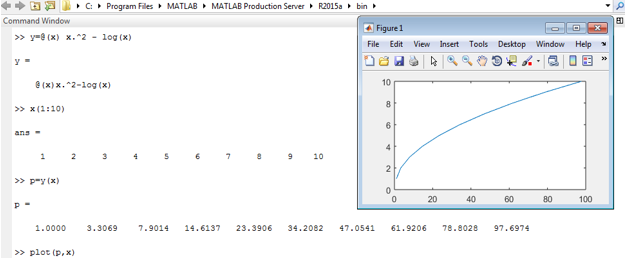
Matlab Code:
clc ;
y = @ ( x ) x.^2 – log(x)
y = @(x)x.^2-log(x)
x (1: 10 )
p = y ( x )
In the above code, x ranges from 0 to 10, so there is no need to assign values of ‘x at the time of compilation, and if discrete values of x and y are known, then we can plot the response of variables x and y. Screen 2 shows the implementation of Example 2 and the response of x and y.
Advantages of Anonymous Functions in Matlab
- In an anonymous function, we can create any function which is not predefined.
- It can be stored in a variable.
- Anonymous functions can be returned in function.
- It can be passed inside the function.
- These functions can not be stored in program files; therefore, we can save memory.
- We can store an anonymous function handle so that we can use it again and again whenever required.
- It is easy to represent and implement.
Conclusion
In Matlab, we can easily implement complex mathematical quadratic equations into a simple form by using anonymous functions. There is no defined name for these functions; we can give any name at the time of definition. The anonymous function saves memory and supports the reusability property; therefore, there is no need to write big and complex expressions repeatedly.
Recommended Articles
This is a guide to Anonymous Functions in Matlab. Here we discuss the steps, advantages of Anonymous Functions in Matlab, and some Examples. You may also look at the following articles to learn more –