Updated March 13, 2023

Introduction to Heap sort in data structure
Heapsort is one of the most efficient algorithms of all the available sorting algorithms, which makes the use of a completely balanced binary tree for visualization of the source array, which is also called a heap. In order to learn and understand the working of the heap, you need to have a clear idea about two data structures, namely – trees and arrays. Also, you should be aware of the data structures like heap and the complete binary tree, which are used for storing the data. This article will learn about the working of heap sort in a data structure along with its implementation in the C++ language.
Working of heapsort
The heap sort technique involves the comparison that is made between the nodes, and it uses the technique of data structure called a binary heap. The heap sort works similar to the selection sort, where we find the smallest element and then the smallest element is placed at the beginning. After that, the same process is carried out for the remaining nodes or elements of the supplied array.
The most used data structure is the binary heap. To understand this, we first need to know what is a complete binary tree has all the levels completely occupied with an allowed exception of the last level. Also, all the elements or nodes in the complete binary tree are placed as left as possible. The binary heap is also one type of special case of a complete binary tree in which the parent node will have the value either greater than both of its child nodes or smaller than both of its child nodes. In the first case, it is called a max heap, while in the latter case, it is referred to as the min-heap. The representation of the heap is done using the binary tree or the array.
Steps for hear sort
The algorithm of heap sort involves the following steps –
- Whatever the supplied input array of data is done, create a max heap from that data.
- Consider that the largest value is stored at the root node of the heap for now. After this, keep on replacing the root node with the last node and decreasing the heap’s size by 1. The last step will be to prepare the heap (heapify) for the root of the tree.
- Follow step 2 unless the heap size is greater than 1.
Note that we can perform the heapify process for a particular node only if all the child nodes of that node are heaped. Hence, while doing this process, the bottom-up approach is followed.
Consider the following heap shown in the diagram –
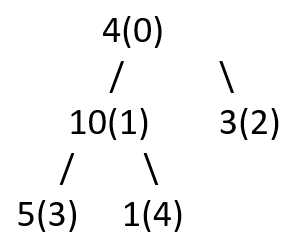
The index of each node is represented in parenthesis after the value of the node. When we carry out the heaping process on the node with index 1, the tree will look as follows –
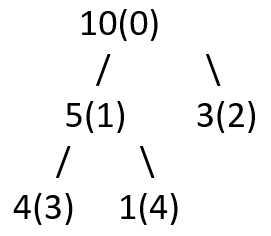
We have to keep on repeating the above process of creating the heap recursively in the top-down approach to create a sorted heap out of it.
Example of Heap sort in data structure
Let us consider an example of how the heap sort actually works using the C++ programming language.
// C++ Program which demonstrates the use of the heap sort and its implementation
#include <iostream>
using namespace std;
/* When a subtree having the root as node i then we have
to prepare the heap of the array with index i of the
node where the size of the array is n*/
void prepareHeap(int arr[], int n, int i)
{
int largest = i; // Create a variable for storing the largest value as root
int l = 2 * i + 1; // left side node
int r = 2 * i + 2; // right side node
// In case if left child has the value which is greater than that of root node
if (l < n && arr[l] > arr[largest])
largest = l;
/* In case if right child has the value which is greater
than that of largest node detected uptil now*/
if (r < n && arr[r] > arr[largest])
largest = r;
// In case if the largest value identified is not the root node
if (largest != i) {
swap(arr[i], arr[largest]);
// Prepare the heap recursively for the sub tree which has got affected.
prepareHeap(arr, n, largest);
}
}
// The function which will carry out the heap sort
void heapSortAlgo(int arr[], int n)
{
// Do the rearragement of the array to create heap
for (int i = n / 2 - 1; i >= 0; i--)
prepareHeap(arr, n, i);
// Retrieve an element one by one from the heap
for (int i = n - 1; i > 0; i--) {
// Shift the current root node at the end
swap(arr[0], arr[i]);
// Prepare the heap for maximum value on the reduced heap
prepareHeap(arr, i, 0);
}
}
/* The function which will print all the contents of the array on the console */
void display(int arr[], int n)
{
for (int i = 0; i < n; ++i)
cout << arr[i] << " ";
cout << "\n";
}
// Controller for calling the functions and deciding the flow
int main()
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
int n = sizeof(arr) / sizeof(arr[0]);
heapSortAlgo(arr, n);
cout << "Using heap sort the generated sorted array is \n";
display(arr, n);
}
The output of the execution of the above program in C++ language is as shown below –
![]()
Time complexity
The time complexity of the heap sort is O(nlogn). On the other hand, when the individual heapify process of creating a new heap with a particular node is considered, then the time complexity for it is O(logn).
Conclusion – Heap sort in data structure
The heap sort works internally in the binary heap, which is a completely balanced binary tree that either has the largest value or the smallest value at its node. Thus, the heapify process is carried out recursively to get the sorted array, as shown in the above example.
Recommended Articles
This is a guide to Heap sort in data structure. Here we discuss the working of heap sort along with its implementation in the C++ language. You may also look at the following articles to learn more –

