Updated March 16, 2023
Introduction to Heap Sort in C
Sorting is a technique that is all about the ordering of elements based on different properties. (Properties like arranging data in ascending, descending or alphabetical orders). One major example of sorting that we can think of here is the ordering of items during online shopping. We can relate to prices, popularity, latest and so on. So there are many techniques for this positioning of elements through sorting. In this topic, we are going to learn about Heap Sort in C.
Here we are going to learn one of the most common sorting techniques, Heap Sort, through C programming language.
The logic for Heap Sort
How actually can we perform heap sort? Let’s check out below.
Firstly, the heap is one of the tree-based data structure. The tree involved here is always a Complete Binary Tree. And, there are two kinds of heap
- Min – Heap: Generally arranged in ascending order, that is if the parent node element is having a value less than that of child node elements.
- Max – Heap: Generally arranged in descending order, that is if the parent node element is having value more than that of child node elements.
Steps for Heap Sort
- Once an unsorted list data is obtained, elements are organized in the heap data structure either based on creating a min-heap or a max-heap.
- The first element from the above list is added into our array
- Again forming the head data structure technique same as the first step is followed and again either the highest element or the least element is picked up and added into our array.
- Repeated steps help us getting the array with the sorted list.
Program for Heap Sort in C
Code:
#include <stdio.h>
int main()
{
int h[20],num,i,j,root,t,x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h[i]);
// build max heap
for(i=0;i<num;i++)
{
x=i;
do
{
root = (x - 1) / 2;
if (h[root] < h[x])
{
t = h[root];
h[root] = h[x];
h[x] = t;
}
x = root;
} while (x != 0);
}
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h[i]);
for (j = num - 1; j >= 0; j--)
{
t = h[0];
h[0] = h[j];
h[j] = t;
root = 0;
do
{
x = 2 * root + 1;
if ((h[x] < h[x + 1]) && x < j-1)
x++;
if (h[root]<h[x] && x<j)
{
t = h[root];
h[root] = h[x];
h[x] = t;
}
root = x;
} while (x < j);
}
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h[i]);
}First, we are asking the user to input the number of elements that are taken for sorting and then the user is allowed to enter different elements that are to be sorted.
Steps Followed
- The next which we are focusing on is to create a heap array, in this case, max-heap array.
- The main condition for getting a max – heap array is to check that no parent node value is less than its child node value. We are going to swap until we achieve that condition.
- The main advantage in this complete binary tree is, the left and right child nodes of a parent node can be accessed with values 2(i) + 1 and 2*(i) + 2 values respectively. Where i is the parent node.
- So, through that way here, we are placing our root node which contains the maximum value in the rightmost leaf node place. And then again following the same procedure such that the next maximum number now becomes the root node.
- We are going to follow the same procedure until only one node is left in the heap array.
- And then, we are arranging our heap array to form a perfect sorted array in increasing order.
- Finally, we are printing the sorted array in the output.
Output:
The output is attached below.
Let me show you the pictorial representation of the happenings:
- The data entered is first represented in the form of a single-dimensional array as follows.
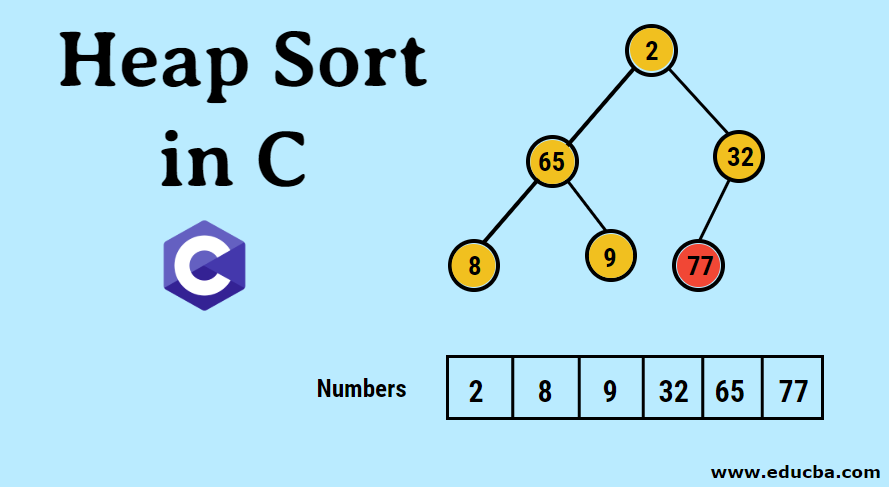
- The pictorial representation of the binary tree formed is as follows:
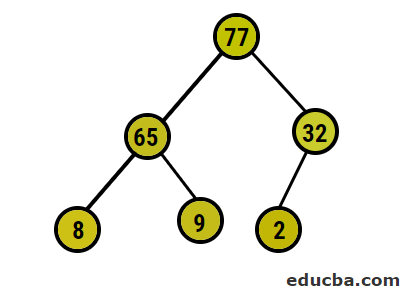
- Now, we are going to convert to the max heap by making sure that all the parent nodes are always greater than child nodes. As mentioned in the output under heap sorted array, the pictorial representation would be:
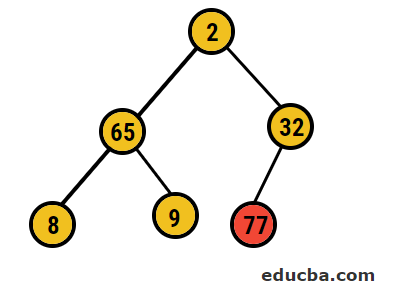
- After this, we are going to swap the root node with the extreme leaf node and then delete it from the tree. The leaf node would be the root now and again same process e followed to again get the highest element in the root
- So, in this case, 77 digits are being deleted from this tree and placed into our sorted array and the process is repeated.
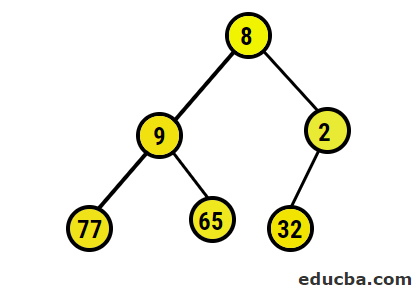
The above we have seen it for forming max heap array. The same process is dealt with with the min-heap array formation also. As discussed above, the only difference is with the relationship between parent and child node elements.
As an exercise, can you try forming the heap sort in descending order?
Conclusion
Though there are many sorting techniques, heap sort is considered one of the better sorting technique due to its time and space complexity. The time complexity for all best, average, and worst case is O(nlogn), where worst-case complexity is better than worst-case complexity of Quicksort and space complexity is O(1).
Recommended Articles
This is a guide to Heap Sort in C. Here we discuss the logic and the Steps for Heap Sort with the sample code and output along with pictorial representations. You may also have a look at the following articles to learn more –