Updated July 24, 2023

Table of Content
What is the Future Value of an Annuity Formula?
The term “annuity” refers to the series of successive equal payments that are either received by you or paid by you over a specific period of time at a given frequency. Consequently, “future value of annuity” refers to the value of these series of payments at some future date.
Now, the future value of annuity are of two types:
- Future Value of The Ordinary Annuity
- Future Value of An Annuity Due
For the future value of the ordinary annuity (FVA Ordinary), the payments are assumed to be at the end of the period, and its formula can be mathematically expressed as,
Where,
- P: Periodic Payment
- n: Number of Periods
- i: Effective Rate of Interest
For the future value of annuity due (FVA Due), the payments are assumed to be at the beginning of the period, and its formula can be mathematically expressed as,
Example of Future Value of an Annuity Formula (With Excel Template)
Let’s take an example to understand the Future Value of an Annuity’s calculation in a better manner.
Future Value of an Annuity Formula – Example #1
Let us take the example of Stefan, who is planning to invest $10,000 annually for the next 10 years at a 5% interest rate in order to save money that is adequate for his son’s education. Calculate the money that Stefan will be able to save in case each deposit is made at the:
- End of The Year
- Beginning of The Year
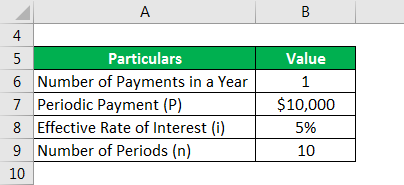
Solution:
FVA Ordinary is calculated using the formula given below
FVA Ordinary = P * [(1 + i)n – 1] / i
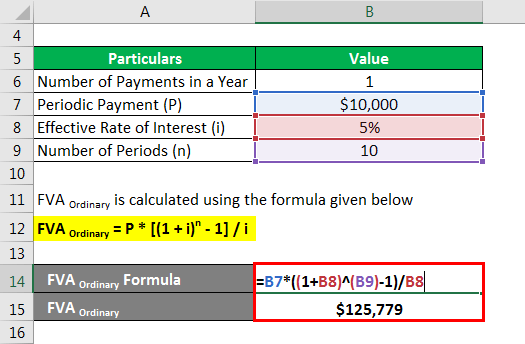
- FVA Ordinary = $10,000 * [(1 + 5%)10 – 1] / 5%
- FVA Ordinary = $125,778.93 ~ $125,779
FVA Due is calculated using the formula given below
FVA Due = P * [(1 + i)n – 1] * (1 + i) / i
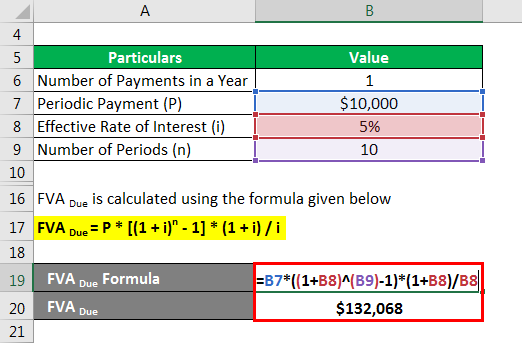
- FVA Due = $10,000 * [(1 + 5%)10 – 1] * (1 + 5%) / 5%
- FVA Due = $132,067.87 ~ $132,068
Therefore, Stefan will be able to save $125,779 in case of payments at the end of the year or $132,068 in case of payments at the beginning of the year.
Future Value of an Annuity Formula – Example #2
Let us take another example where Lewis will make a monthly deposit of $1,000 for the next five years. If the ongoing rate of interest is 6%, then calculate
- Future value of the Ordinary Annuity
- Future Value of Annuity Due
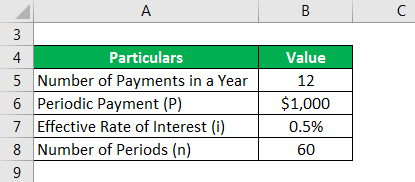
Solution:
FVA Ordinary is calculated using the formula given below
FVA Ordinary = P * [(1 + i)n – 1] / i
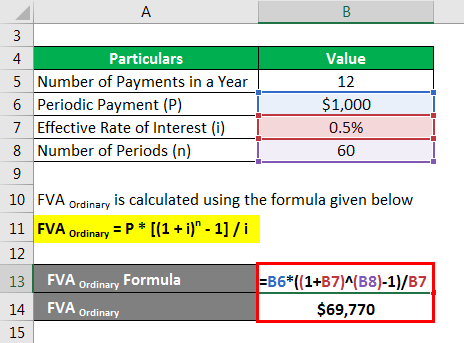
- FVA Ordinary = $1,000 * [(1 + 0.5%)60 – 1] / 0.5%
- FVA Ordinary = $69,770.03 ~ $69,770
FVA Due is calculated using the formula given below
FVA Due = P * [(1 + i)n – 1] * (1 + i) / i
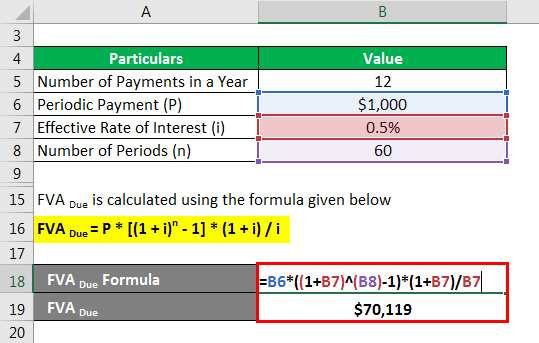
- FVA Due = $1,000 * [(1 + 0.5%)60 – 1] * (1 + 0.5%) / 0.5%
- FVA Due = $70,118.88 ~ $70,119
Therefore, Lewis is expected to have $69,770 in case of payment at month-end or $70,119 in case of payment at month start.
Explanation
The formula for Future Value of an Annuity formula can be calculated by using the following steps:
Step 1: Firstly, calculate the value of the future series of equal payments, which is denoted by P.
Step 2: Next, calculate the effective rate of interest, which is basically the expected market interest rate divided by the number of payments to be done during the year. I denote it.
Step 3: Next, calculate the total number of periods for which the payment is to be made, and it is computed as the product of the number of years and number of payments to be made in a year. It is denoted by n.
Step 4: Finally, in case the payments are to be made at the end of the period, then the future value of the ordinary annuity formula should be calculated using the value of the series of payments (step 1), interest rate (step 2) and payment period (step 3) as shown below.
FVA Ordinary = P * [(1 + i)n – 1] / i
On the other hand, in the case of payments at the beginning of the period, then the future value of the annuity due formula should be calculated using the value of the series of payments (step 1), interest rate (step 2) and payment period (step 3) as shown below.
FVA Due = P * [(1 + i)n – 1] * (1 + i) / i
Relevance and Use of Future Value of an Annuity Formula
The concept of the future value of the annuity is an interesting topic as it captures the time value of money and how the timing of payment during a given period makes a difference to the overall future value of money. An annuity’s future value is primarily used in computing premium payments of life insurance policy, calculation of monthly contribution to provident fund, etc.
Future Value of an Annuity Formula Calculator
You can use the following Calculator
| P | |
| i | |
| n | |
| FVAOrdinary | |
| FVAOrdinary = | P * [(1 + i)n - 1] / n | |
| 0 * [(1 + 0)0 - 1] / 0 = | 0 |
Recommended Articles
This is a guide to the Future Value of an Annuity Formula. Here we discuss how to calculate the Future Value along with practical examples. We also provide a calculator with a downloadable excel template. You may also look at the following articles to learn more –

