Updated March 17, 2023

Introduction to Fibonacci Series
Fibonacci series lies in the process that each number acts to be a sum of two preceding values and the sequence always starts with the base integers 0 and 1. Fibonacci numbers are muscularly related to the golden ratio. In this topic, we are going to see about the Fibonacci Series in Java.
Formula:
| Fibonacci series for first 21 numbers | ||||||||||||||||||||
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 | F16 | F17 | F18 | F19 | F20 |
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | 987 | 1597 | 2584 | 4181 | 6765 |
Key Applications
Here are the Key applications of the Fibonacci Series in Java given below:
- Miles to kilometer and kilometer to miles conversion.
- Some instances of Agile methodology.
- Euclid’s algorithm run time analysis computation is carried out using this series technique.
- Fibonacci statistics are worn mathematically by some pseudorandom number generators.
- The poker planning process involves the use of this technique.
- The data structure technique of the Fibonacci heap is achieved using the Fibonacci series technique.
- In optics, whilst a shaft of light gleam at a point of view from beginning to end of two piled translucent plates of dissimilar materials of dissimilar refractive indexes, it may return off three surfaces: the pinnacle, center, and base surfaces of the two plates. The numeral of dissimilar ray path to have kreflections, for k > 1, is the {\display style k} the Fibonacci number.
Fibonacci Series Program (Non recursive program)
Following is a Fibonacci series program:
Code:
// Fibonacci series program
public class Fibonacci {
// main program
public static void main(String[] args) {
int count = 10, var1 = 0, var2 = 1;
System.out.print("First " + count + " terms: ");
// Fibonacci series formation loop
for (int i = 1; i <= count; ++i)
{
System.out.print(var1 + " + ");
int added_sum= var1 + var2;
var1 = var2;
var2 = added_sum;
}
}
}Output:
![]()
Explanation:
- This program calculates the Fibonacci series for a given range of numbers.
- Here this process is achieved using no recursive technique.
Program Algorithm
- A root class Fibonacci is declared with the necessity that all program codes embedded into this class will address the functionality of achieving a Fibonacci series of numbers.
- Inside the root class, the main method is declared. The main method acts, as a rule, as a significant Java method. The JVM execution will not take place without the presence of the main method in the program. The explanation of various sub-components of the main method is expressed below,
- Next, the variable initialization section is implied. This section involves the initialization of three different variables. Two among them are for achieving the Fibonacci logic through a variable level value swap, and another variable is applied for regulating the count of values for which the Fibonacci logic needs to be generated.
- The Fibonacci series program’s key logic is achieved using the below given for loop in the program section.
Code:
for (int i = 1; i <= count; ++i)
{
System.out.print(var1 + " + ");
int added_sum= var1 + var2;
var1 = var2;
var2 = added_sum;
}- The logic behind this for the loop section is as follows; initially, a range of values is being performed on a loop; the loop happens with an increment on the range value for every flow. Additionally, in every flow, the two swap variables’ value is summed up into a third variable.
- After summing up, the second variable value is implied into the first variable, so this makes the first variable value to be flushed away from this process. In the next step, the summed value is assignated to the second variable.
So at the end of this instance, for a single logic flow, the below happenings are applied:
- The value of the first variable is flushed away.
- The existing second variable value is filled in the first variable.
- The summed up value is moved in into the second variable.
In the process of performing the below logic sequence for the given count of values the need, the Fibonacci series can be achieved.
1. Fibonacci Series Program (Using Arrays)
Code:
import java.util.Arrays;
public class Main {
public static void main(String[] args) {
int Count = 15;
long[] array = new long[Count];
array[0] = 0;
array[1] = 1;
for (int x = 2; x < Count; x++) {
array[x] = array[x - 1] + array[x - 2];
}
System.out.print(Arrays.toString(array));
}
}Output :
![]()
Explanation:
- Implying the program logic drafted above, but at this instance, the Fibonacci inputs are stored as part of arrays.
- So all operations mentioned above are carried out concerning an array.
2. Fibonacci Series Program (Without Implying Any Loops)
Code:
public class Fibonaccifunction
{
private static int indexvalue = 0;
private static int endPoint = 9;
public static void main (String[] args)
{
int number1 = 0;
int number2 = 1;
fibonaccifunction(number1, number2);
}
public static void fibonaccifunction(int number1, int number2)
{
System.out.println("index value : " + indexvalue + " -> " + number1);
if (indexvalue == endPoint)
return;
indexvalue++;
fibonaccifunction(number2, number1+number2);
}
}Output :
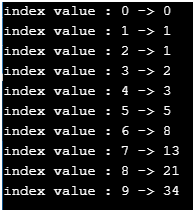
Explanation:
- Implying the program logic drafted above but at this instance, the Fibonacci inputs handled recursively using a function named Fibonacci.
3. Fibonacci Series Program (Without implying Any loops but Achieved only using Conditions)
Code:
public class Fibonacci_with_conditions
{
static int number2=1;
static int number1=0;
static int next=0;
public static void Fibonacci_conditions( int number)
{
if(number<10)
{
if(number == 0)
{
System.out.print(" "+number);
number++;
Fibonacci_conditions (number);
}
else
if(number == 1)
{
System.out.print(" "+number);
number++;
Fibonacci_conditions(number);
}
else{
next=number1+number2;
System.out.print(" "+next);
number1=number2;
number2=next;
number++;
Fibonacci_conditions(number);
}
}
}
public static void main(String[] args)
{
Fibonacci_conditions(0);
}
}Output:
![]()
Explanation:
- Implying the program logic drafted above, but at this instance, the Fibonacci inputs are regulated only through necessary conditional statements.
- According to the conditions, the swapping of the variables is necessarily carried out.
4. Fibonacci Series Program( Without Loops, the Concepts of Looping is Achieved using Nextint Method)
Code:
import java.util.*;
public class Fibonacci_series
{
public static void main(String[] args)
{
System.out.println("Input:");
int number= 10,value1=1,value2=0,value3=0;
num(number, value1, value2, value3);
}
public static void num(int number,int value1,int value2,int value3)
{
if(value1 <= number)
{
System.out.println(value1);
value3=value2;
value2=value1;
value1=value2+value3;
num(number,value1,value2,value3);
}
}
}Output:
![]()
Explanation:
- Implying the program logic drafted above, but at this instance, the Fibonacci inputs are handled recursively using a function named num, and the loop is carried out using the nextInt function.
Conclusion – Fibonacci Series in Java
These programs are implied to achieve the Fibonacci series for a given integer value. A largely classified set of techniques are implied in the given list of examples. Techniques like an array-oriented approach and a condition-alone approach are very much peculiar.
Recommended Articles
This is a guide to Fibonacci Series in Java. Here we discuss the fibonacci series and a set of techniques that are implied in the given list of examples. You may also look at the following article to learn more –


