Introduction to Exponential Search Algorithm
Exponential Search is a search algorithm crafted to pinpoint an element within a sorted array efficiently. Unlike linear or binary search, which necessitates sorting the array, exponential search particularly shines in scenarios where the array’s size is unknown or unbounded. The algorithm harnesses the principles of binary search. Still, with a crucial optimization, it establishes a range where the target element might be located by exponentially increasing the interval size with each iteration. This approach empowers the algorithm to narrow the search space swiftly, rendering it highly effective for sizable arrays. While it may share resemblances with binary search, exponential search diverges significantly in its methodology, presenting advantages in specific situations, notably when handling unbounded arrays or when the target’s position is closer to the array’s beginning.
Table of Contents
How Exponential Search Works
- Determining the Initial Range:
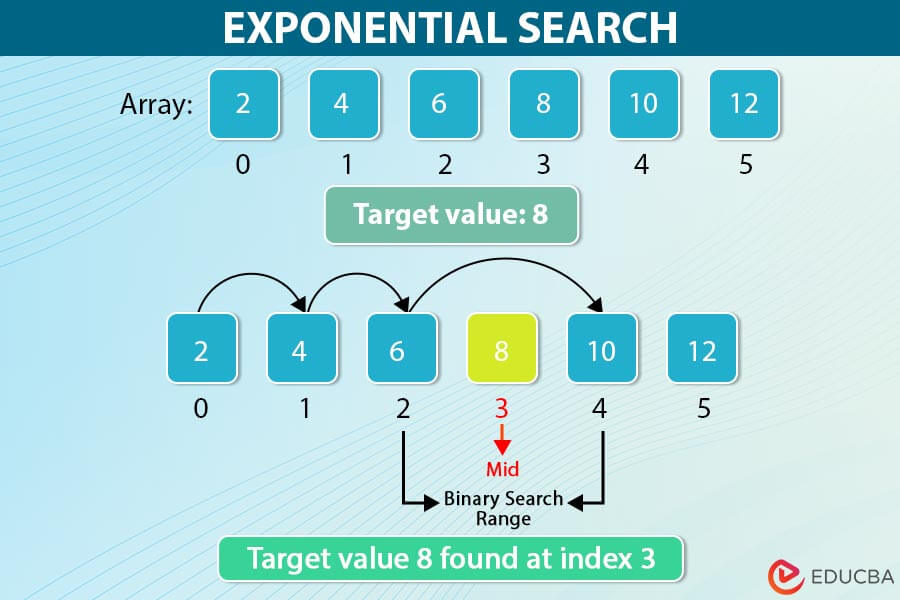
It begins by inspecting the first element of the array. If this element matches the target value, the search ends immediately with the element found at index 0. Otherwise, the algorithm sets an initial interval (or range) to search within. This interval is determined by repeatedly doubling the index until encountering a value larger than the target or reaching the end of the array.
For example, if the array size is n, the algorithm might start with index 0 and double it successively until it surpasses the last index of the array.
- Performing Binary Search within the Range:
Once the initial range is determined, Exponential Search employs binary search within this narrowed-down interval. Binary search functions by continually dividing the search interval in half and determining which half the target might lie in. This process continues until the target element or the interval becomes empty.
- Completing the Search:
If the binary search phase finds the target element successfully, the algorithm returns its index. However, suppose the binary search concludes with an empty interval, indicating that the target element is not present in the array. In that case, the algorithm identifies this absence and returns a predefined “not found” value.
Understanding the Algorithm
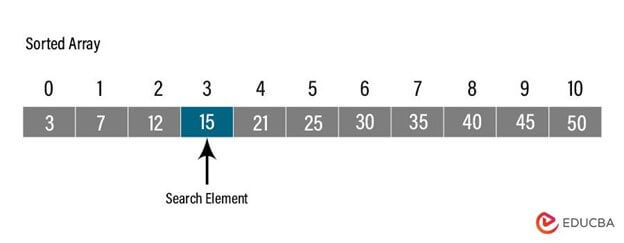
- Let’s say we have a sorted array of integers:
We want to find the index of element 15.
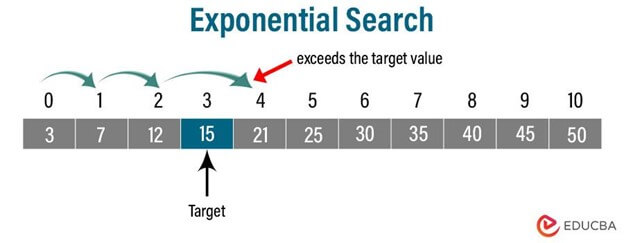
- The algorithm begins by examining the first element of the array, which is 3. Since this element is not the target element, it doubles the index to 1. This process will continue until the target element is found.
Starting with index 0 (value: 3), the algorithm doubles the index to 1 (value: 7), then to 2 (value: 12), and finally to 4 (value: 21).
- Here, the element at index 4 (21) exceeds our target value (15). So, the algorithm sets the initial range between index 1 and index 4.
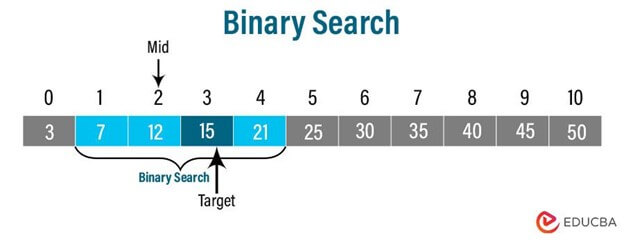
- The algorithm performs a binary search within this narrowed-down interval (from index 1 to index 4).
The binary search phase considers the interval [7, 12, 15, 21]. It compares the target value (15) with the middle element (index 2, value: 15) and finds a match.
- The algorithm successfully locates the target element (15) at index 2 and returns this index as the result.
Time Complexity Analysis
- Best Case: The best-case scenario occurs when the target element is found during the exponential search phase, typically at the very beginning of the array. In this case, the algorithm requires only a constant number of comparisons to locate the target element. Hence, the best-case time complexity is O(1).
- Worst Case: The worst-case scenario arises when the target element is located towards the end of the array, necessitating the maximum number of iterations during the exponential search phase. The number of iterations is determined by the index (let’s call it i) of the element exceeding the target value. Consequently, in the worst case, the time complexity of the exponential search phase is O(log i). Additionally, the binary search phase within the identified range has a time complexity of O(log m), where m is the size of the interval. Therefore, the total worst-case time complexity of Exponential Search is the sum of the complexities of both phases: O (log i) + O(log m).
Space Complexity Analysis
Exponential Search maintains a space complexity of O(1), denoting a constant need for extra memory irrespective of the array’s size. This complexity arises from the algorithm’s use of several variables to manage indices and values throughout its execution. Consequently, its memory usage remains consistent, offering efficiency regardless of input array dimensions.
Implementation
Pseudocode
function exponentialSearch(arr, target):
n := length of arr
if arr[0] is target:
return 0 // Element found at the beginning
index := 1
while index < n and arr[index] <= target:
index := index * 2
start := index / 2
end := min(index, n - 1)
return binarySearch(arr, target, start, end)
function binarySearch(arr, target, start, end):
while start <= end:
mid := start + (end - start) / 2
if arr[mid] is target:
return mid // Element found
else if arr[mid] < target:
start := mid + 1 // Search right half
else:
end := mid - 1 // Search left half
return -1 // Element not foundExplanation:
- The exponential Search function initiates by determining the array’s length and checking if the target is at the array’s beginning.
- If not, it incrementally doubles the search index until it either exceeds the array size or finds a value greater than the target.
- The algorithm then defines the search range based on the last successful index and calls binarySearch to perform a binary search within this range.
- The binarySearch function compares the target with the middle element, adjusts the search range accordingly, and repeats until it finds the target or exhausts the range.
- If it finds the target, it returns its index; otherwise, it returns -1 to indicate its absence.
Example
Code:
def exponential_search(arr, target):
n = len(arr)
if arr[0] == target:
return 0 # Element found at the beginning
index = 1
while index < n and arr[index] <= target:
index *= 2
start = index // 2
end = min(index, n - 1)
return binary_search(arr, target, start, end)
def binary_search(arr, target, start, end):
while start <= end:
mid = start + (end - start) // 2
if arr[mid] == target:
return mid # Element found
elif arr[mid] < target:
start = mid + 1 # Search right half
else:
end = mid - 1 # Search left half
return -1 # Element not found
# Example usage:
arr = [4, 12, 19, 22, 31, 35, 43, 49, 56, 63]
target = 43
result = exponential_search(arr, target)
if result != -1:
print(f"Element {target} found at index {result}")
else:
print(f"Element {target} not found")Output:
Time Complexity:
O(log i) + O(log m)
Pros and Cons of Exponential Search
Pros
- Efficient for Unbounded Arrays: It performs well in scenarios where the array size is unknown or unbounded. Its ability to dynamically adjust the search interval based on exponential growth allows it to handle large arrays without prior knowledge of their size.
- Adaptable to Sorted and Unsorted Arrays: Unlike some search algorithms that require sorting the array, Exponential Search can efficiently locate the target element even in unsorted arrays. It adjusts the search interval dynamically, allowing it to work effectively regardless of the array’s soreness.
- Guaranteed to Find the Element: Exponential Search will successfully locate the target element within the array if it exists. In the worst case, it returns to a linear search within the identified range, ensuring the target’s location.
- Simplicity of Implementation: It is relatively easy to implement compared to other search algorithms. Its straightforward approach, combining exponential growth for range determination and binary search within the identified range, makes it accessible for implementation in various programming languages.
Cons
- Lower Efficiency Compared to Binary Search: Although Exponential Search offers benefits for unbounded arrays, it tends to be less efficient than binary search in scenarios with relatively small, known array sizes, resulting in slightly slower performance.
- Requirement for Random Element Access: It relies on random access to array elements, making it unsuitable for scenarios where such access is unavailable.
- Performance Degradation with Large Arrays: In scenarios featuring large yet bounded array sizes, Exponential Search may experience performance degradation due to the extensive comparisons required during the exponential search phase.
- Dependence on Pre-Sorting: While Exponential Search can handle unsorted arrays, optimal performance hinges on pre-sorting. Without it, the algorithm’s efficiency may decline, especially when the target element positions near the array’s end.
Real World Applications
- Database Searching: It can be employed in database systems to efficiently search through large datasets, primarily when one doesn’t know the database size or encounters unsorted data. It offers a viable alternative to traditional search methods and can expedite query processing, mainly when quick access to relevant data is crucial.
- File System Searching: File systems often contain vast amounts of data across directories and subdirectories. You can use Exponential Search to look for particular files or directories within the file system, providing a mechanism for efficiently navigating the file structure. It is beneficial in file management systems where users need to locate files or directories quickly.
- Network Routing: In networking applications, routers and switches must efficiently route packets through networks comprising numerous nodes and links. Exponential Search can efficiently explore the network topology to identify the most efficient route for packet routing, potentially enhancing network performance and reducing latency, improving the overall quality of service.
- Genetic Sequence Analysis: In genetic sequence analysis, researchers can utilize Exponential Search to search for specific patterns or sequences within DNA or protein sequences. By efficiently scanning vast genomic datasets, Exponential Search enables researchers to identify relevant genetic markers or sequences associated with various biological phenomena, contributing to advancements in medicine and agriculture.
- Search Engines: Search engines employ sophisticated algorithms to index and retrieve relevant web pages in response to user queries. Exponential Search can be incorporated into the indexing and retrieval processes to efficiently locate relevant web pages based on search terms or keywords. By optimizing search operations, Exponential Search enhances the speed and accuracy of search engine results, thereby improving the user experience.
Conclusion
It offers a versatile and efficient approach to searching for elements within arrays, particularly in scenarios where the array size is unknown or unbounded. By dynamically adjusting the search interval based on exponential growth, Exponential Search can efficiently locate target elements, even in unsorted arrays. Despite its simplicity and adaptability, Exponential Search may not always be the optimal choice compared to other search algorithms like binary search, especially when dealing with relatively small and sorted arrays. However, it excels in scenarios with large and unknown array sizes, making it suitable for various real-world applications such as database searching, file system navigation, network routing, genetic sequence analysis, and search engines. Overall, its adaptability, simplicity, and reliability make it a valuable addition to the arsenal of search techniques, particularly in situations where quick access to data is paramount and the array size is unpredictable.
Frequently Asked Questions (FAQs)
Q1. When should I use Exponential Search?
Answer: It proves valuable when the array size remains uncertain or unbounded, given its capability to dynamically adapt the search interval. It finds applications across various domains, including database querying, file system traversal, network routing, genetic sequence analysis, and search engine functionality.
Q2. Does Exponential Search require the array to be sorted?
Answer: Although Exponential Search can operate on unsorted arrays, the optimized performance of Exponential Search occurs with sorted arrays. Prior sorting of the array can enhance its efficiency by minimizing the number of comparisons needed during the search procedure.
Q3. How does Exponential Search handle empty arrays or arrays with only one element?
Answer: It manages empty arrays or arrays with a solitary element by promptly establishing whether the target value is absent (in the instance of an empty array) or by directly comparing it with the single array element. In either scenario, the search concludes swiftly, resulting in either a successful find or a confirmation of absence.
Q4. Can Exponential Search be applied to multidimensional arrays?
Answer: Primarily, developers design Exponential Search for searching within one-dimensional arrays. While it’s theoretically feasible to expand its application to multidimensional arrays, doing so would entail greater complexity and reduced efficiency than using specialized search algorithms designed for multidimensional data structures.
Recommended Articles
We hope that this EDUCBA information on “Exponential Search ” was beneficial to you. You can view EDUCBA’s recommended articles for more information,