Updated April 10, 2023
Introduction to Execute Shell Script
Continuing the momentum of the understanding shell script in detail, in this article we would understand how the execution of shell scripting is done and some details which need to be kept in mind while executing the same. We already have learned about different other aspects of shell scripting like arrays in the shell script, arguments in the shell script, and until and unless we know how to execute a shell script all other technical nit bits are of no use in learning. One kind of gets handicapped if one user is not able to execute a shell script, prevailing to some details which need to be kept in mind which we will go through in detail in this article. For reference, in the entire article, we would be looking into aspects of how we execute a shell script in a Linux or UNIX operating system. So, without much further ado, let us get started!
What is Execute Shell Script?
Before we jump into the execution of shell script, let us take some time to revise the fundamentals of shell scripting. Shell scripts have an extension of .sh consisting of bash and Korn constructs supported through programming and finally saved as scripts. When executed in a Linux or UNIX environment, these scripts turn into shell commands and then gets executed in the environment. In case you are one of the system administrators, it becomes mandatory for you to have knowledge on scripting, as it will help you understand and figure out intricate details of how the applications start, upgrades maintain, or gets removed. Not only this but it also essentially makes you understand the entire details of the user environment are built.
In shell scripting, there are numerous topics that enable it to perform the required task using shell scripts. Some of these are loops, parameter scripting, parameter shifting, getopts, case, eval, etc. Now, let us start with the basic question, of how does a user runs a shell script in a Linux operating system. Below mentioned are the steps which will enable us to successfully execute a shell script. For reference, we would name the shell file as sampleShellScriptEduCBA.sh
1. The first and foremost step is to enable the script to execute permission. There are few particular permissions given to a file namely, read, write, and execute.
For a script to be executable one should allow the file to do so by:
- chmod +x sampleShellScriptEduCBA.sh
2. Once the script has to be allowed for execution the next step is to run the shell script. For this, there are 3 alternatives and there is no preference on which one we should use. It depends entirely on the usage comfortability of the user who wants to run the script.
The three alternatives are:
- ./sampleShellScriptEduCBA.sh
- sh sampleShellScriptEduCBA.sh
- bash sampleShellScriptEduCBA.sh
One would now think is it that simple to run a shell script. Well yes! Absolutely. There is no rocket science behind running a shell script. But in the course of executing a shell script, one needs to be vigilant about few steps we would discuss in this section or maybe in the example section so that the photographic memory of these will pull you to this article again in case of any dilemma in running a shell script.
The first and foremost essentiality is running the shell script as a root user. In some cases, it is extremely essential to run a shell script as root user because without the root access installing an application or making modifications at a system level might not be possible by just running the script from a user which has no root access. In case, the user itself is a root user, this step might not be valid. For running the shell script as root user on needs to use sudo before starting to execute the script.
For example:
sudo bash sampleShellScriptEduCBA.shOnce the above command is executed, you would need to enter the credentials of the root user, i.e. password and the script will execute from there on as a root user.
In addition to the command-line capabilities of running a shell script, there is a provision of running the shell script using a GUI.
For this you would need to:
- Right-click on the shell script file.
- Click on Properties.
- In the permissions, tab click on the checkbox to enable execute
- Once the above changes are done, close the window and then click on the file and select Run in terminal to execute the shell script in the terminal directly.
It might be sometimes extremely necessary that the shell script needs to be run using debugging options. In the likely event of the cases of running the shell script using debug on, we have three options and they are:
- sh -n sampleShellScriptEduCBA.sh
- sh -v sampleShellScriptEduCBA.sh
- sh -x sampleShellScriptEduCBA.sh
In the above three examples, we see only one argument changes and that is the argument that is passed to understand what kind of debug needs to be switched on. For -n, the shell script is commanded to not run the commands inside the script, but instead, the command including -n will check for the syntax. For -v, stands for verbose, we would get the detail of each command prior to the execution. Lastly, for the -x command, one of the most widely used arguments as it gives the execution trace of the shell script hence allowing the user to diagnose the bug.
So, in the next section, we would look at the examples of the previous command line commands to run a shell script along with the desired outputs.
Examples to Implement Execute Shell Script
We have had an in-depth understanding of the theory of commands, but EduCBA always believes in giving a realistic view of what happens if the shell scripts are executed. In this section, we would go through those commands with their outputs.
Example #1
Changing the permission to include execute permission:
Code:
chmod +x sampleShellScriptEduCBA.shPermission Before:

Changing the permission:

The “x” in the left-hand permission details mentions that the shell script sampleShellScriptEduCBA.sh now has executed permission.
Example #2
Running/Executing the script
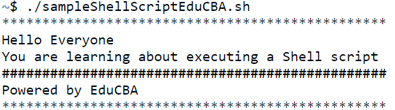
Code #1
/sampleShellScriptEduCBA.shOutput:
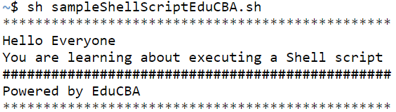
Code #2
sh sampleShellScriptEduCBA.shOutput:
Code #3
bash sampleShellScriptEduCBA.shOutput:
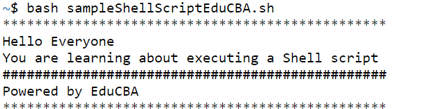
In the above outputs, we can easily compare that there are no visible differences in 3 ways of running a shell script. All that matters is the developer’s preference.
Example #3
Executing script as the root user:
![]()
Example #4
Debugging
Code #1
sh -n helloWorld.shOutput:
![]()
Code #2
sh -v helloWorld.shOutput:

Code #3
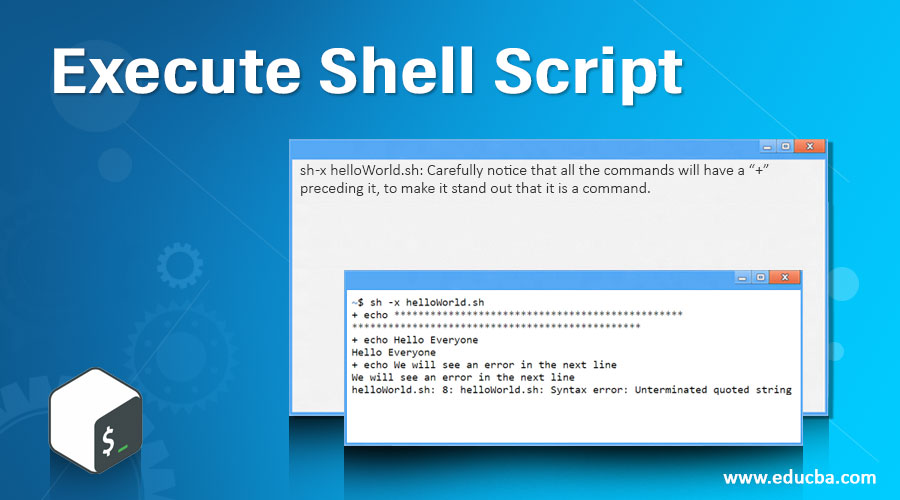
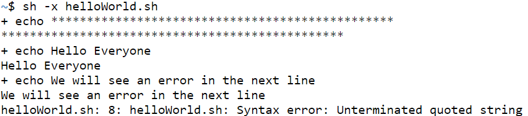
sh -x helloWorld.sh: Carefully notice that all the commands will have a “+” preceding it, to make it stand out that it is a command.Output:
Conclusion
In this article, we were able to deep dive into different aspects of how we would use the command line to execute shell scripts in day to day work. Using a GUI to execute has many restrictions and hence the most preferred way is through the command line. There are a lot of other features that makes the shell script deserve its place in the world of automation and AI to make its mark and be consistent in delivering the output needed from it!
Recommended Articles
We hope that this EDUCBA information on “Execute Shell Script” was beneficial to you. You can view EDUCBA’s recommended articles for more information.


