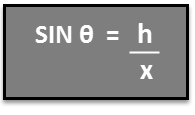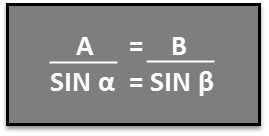Updated May 8, 2023
SIN Function in Excel
The sin function of Excel is another mathematical function that gives the Sine value of any angle or radian value of an angle. We all know that Perpendicular mathematically calculates the Sine angle to Hypotenuse, but that provides the logic of the Sine angle. To calculate the Sin function, we need to feed the value with the radians function or multiply the angle by Pi()/180 to get the actual value.
Basic Trigonometric Function
So, to solve the trigonometric function, Sine provides the SIN function, which is a basic trigonometric function but comes in handy, particularly if you are working in manufacturing Navigation, or Communication Industries. But it is important to note Excel uses radians, not degrees, to calculate any trigonometric expression. There are two ways of going about this:
- Recall that π = 180°. So, if the angle is in degrees, multiply it by π /180° to convert it to radians. In Excel, this conversion can be written PI( )/180. For example, to convert 60° to radians, the Excel expression would be 60*PI( )/180, which equals 1.0472 radians.
- Excel is also equipped with a very useful tool called RADIANS. It accepts an angle as an argument, in which the angle refers to the degrees that have to be transformed into radians. Take the instance where the expression utilized to transform 210° into radians is “RADIANS(210)”, and it evaluates to 66519 radians.
Conversely, the DEGREES utility is equally important. This function can do the exact opposite of the RADIANS function by converting radians to degrees. For example, DEGREES(PI( )/2 ) evaluates 90.
How to Use the SIN Function in Excel?
Let’s understand how to use the SIN Function in Excel by using some examples and real-life illustrations of the SIN Function in Excel.
Example #1
Calculating Sine Value using SIN Function in Excel
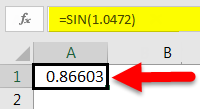
To find the sine of a particular number, we have to first write =SIN() in a particular cell.
As you can see from the above screenshot, the SIN function in Excel expects a number as an input. This number usually represents a value in radians. So, in this case, we will write “=SIN(1.0472)”, where 1.0472 is the radians equivalent of 60 degrees.
Once we do this, we will get the SIN value of 60 degrees.
Example #2
Calculating Sine Value using SIN and RADIAN Function in Excel
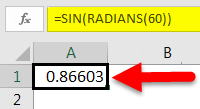
Now let us see how we can use SIN more effectively when we don’t know the exact radian value for a degree. We will use the RADIANS() to find the radian value, which we will pass as an argument to the SIN function. So, we start with the earlier version of the SIN( ):
Next, we will pass RADIANS(60) as an argument to the SIN function, where 60 is the degree value.
As we can see from the example above, RADIANS() accepts a value in degrees. So, we shall pass 60 as the value to RADIANS().
Then Press Enter. This yields the following result.
So, we see that the result is the same as the first example.
Example #3
Calculating Sine Value using SIN and PI Function in Excel
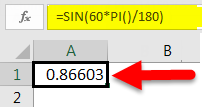
There is yet another way to convert a degree value to radians for our use in the SIN function. We remember from our time in school that π = 180°. So, if the angle is in degrees, multiply it by π/180° to convert it to radians. In Excel, this conversion can be written PI( )/180. For example, to convert 60° to radians, the Excel expression would be 60*PI( )/180, which equals 1.0472 radians.
We begin by writing the SIN function in the same way as above.
Next, we will directly pass 60° as the argument to the SIN function. But this wouldn’t give us the corresponding value of 60 degrees in radians. Hence we will multiply 60 by PI()/180.
This will give us the following result:
As we can see, this is the same as the above examples.
Example #4
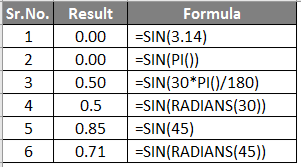
Now, let’s look at another example showing the results of the SIN function for various values.
Explanation of the results shown in the above table:
Case 1 and 2 :
3.14 is the value of Pi, and we can use both methods to get a value of 0. This means the SIN of Pi radians is 0.
Case 3 and 4 :
Radians and Pi/180 have equal values in mathematics, and hence SIN function gives the same value. Both examples imply a SIN of 30 degrees which gives a value of 0.5.
Case 5 and 6 :
By default, SIN 45 = 0.85 is the SIN of 45 radians; excel takes all the angles in radians and not degrees. To convert it into a degree, we can use the radian function and get a SIN of 45 degrees, as shown in the last row. i.e. SIN(RADIANS(45)) = 0.707 or 0.71
Example #5
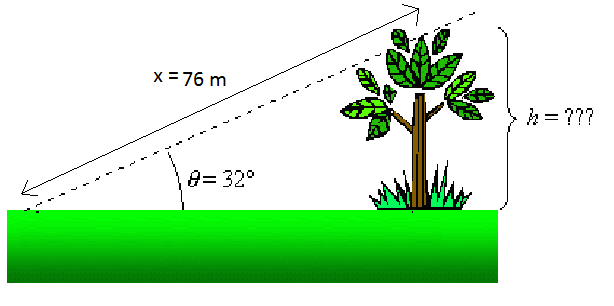
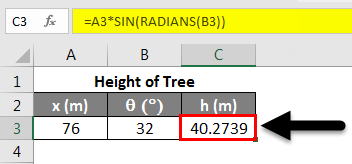
For example, we want to know the tree’s height in the figure above. We know that if we stand 76 m from the top of the tree (x = 76 m), the line of sight to the top is 32° concerning the horizon (θ = 32°).
Hence to solve for the height of the tree h, we find h= x SIN θ. We know that:
The SIN function has only one argument, which is a number. A number is required to calculate the SIN of it. Hence it is vital to convert degrees to a number in radians before finding the Sine of it.
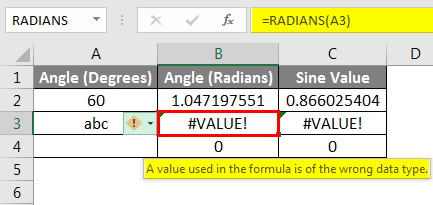
The SIN function displays the #VALUE! Error if the reference used as the function’s argument points to a cell containing text data. In the example below, the cell reference of the third-row points to the text label in Angle (Degrees). Since the SIN functions only support a number as an argument, SIN will evaluate an error, in this case, #VALUE! If the cell points to an empty cell, the function returns a zero value, as shown in the example below. Excel’s trigonometric functions interpret blank cells as zero, and the sine of zero radians equals zero.
Example #6
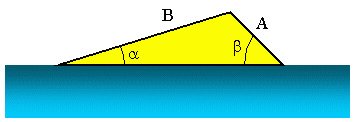
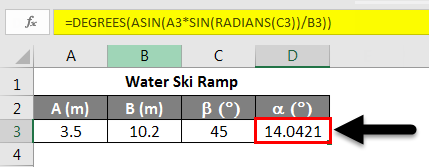
Suppose we find out the launch angle of a water ski ramp as in the figure above. We know that A = 3.5 m, B = 10.2 m, and b = 45.0°. Now to find a, we can use the Law of Sines. In this scenario, it can be written as:
We can re-organize this equation as follows:
Using the arcsine or inverse sine, we can find the angle α. Applying the equation shown below.
Example #7
In our final trigonometric example, we will use Excel to examine the trigonometric identity:
sin²θ + cos²θ = 1
Note that in the screenshot below, this identity holds when θ is given in both radians and degrees.
Note the unit description for the angle θ is placed in different cells than the numbers. If we place the numbers and the units in the same cell, Excel will not be able to differentiate the number from the text, and therefore we will not be able to reference the cells for use in an equation, which would result in #VALUE! Error.
Things to Remember
- Remember that the Excel SIN function works with Radian by default.
- Convert the number required in Radian or Degree using the RADIANS or DEGREES functions.
- You can use the PI() function to get the exact results of the SIN function while working with π.
Recommended Articles
This has been a guide to SIN Function in Excel. Here we discussed How to use the SIN Function in Excel, practical examples, and a downloadable Excel template. You can also go through our other suggested articles –