Updated May 3, 2023
EVEN Function (Table of Contents)
EVEN Function in Excel
EVEN Function converts any Odd number or any number into the nearest even number. The selected number can be a whole number or in decimal. The important thing is that if we feed an even number, it will not be changed, and it only considers numbers.
EVEN Formula in Excel:
Below is the EVEN Formula in Excel :
EVEN Formula includes only one argument.
- Number: The required parameter converts the supplied number to the nearest even number.
How to Use EVEN Function in Excel?
This is very simple and easy to use. Let us understand the working of the EVEN Function in Excel with some examples.
Example #1
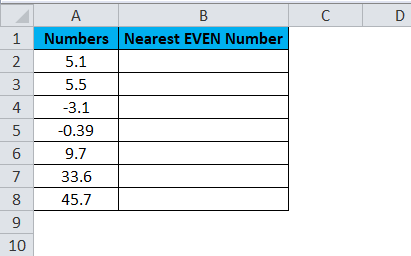
In this example, Convert the below-given numbers to the nearest EVEN number. Enter these numbers from A2:A8 and
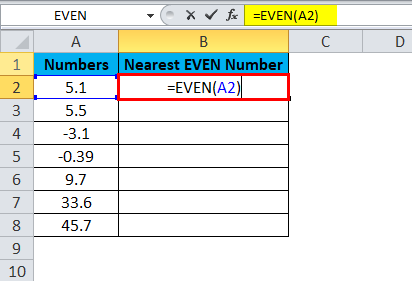
And apply the even formula in cell B2.
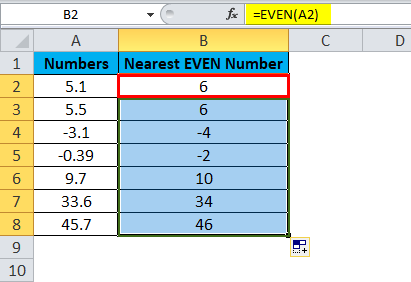
Now drag and drop the formula to the remaining cells.
Now, look at each example one by one.
- Firstly the value we are converting is 5.1, and the nearest EVEN integer value is 6. It cannot be 4 because the difference between 5.1 and 4 is (5.1 – 4 = 1.1) 1.1, but the difference between 5.1 and 6 is (5.1 – 6 = 0.9) 0.9. So the closest EVEN integer number is 6.
- The same logic applies to the second one as well.
- For the third value, a negative even number for -3.1 is 4. It is because the nearest integer EVEN number is 4, not 2.
- The fourth one is -0.39; the first-ever EVEN number is -2. Therefore, the formula has returned -2 as a result.
Like this EVEN formula, round up the given number to the nearest EVEN number.
Example #2
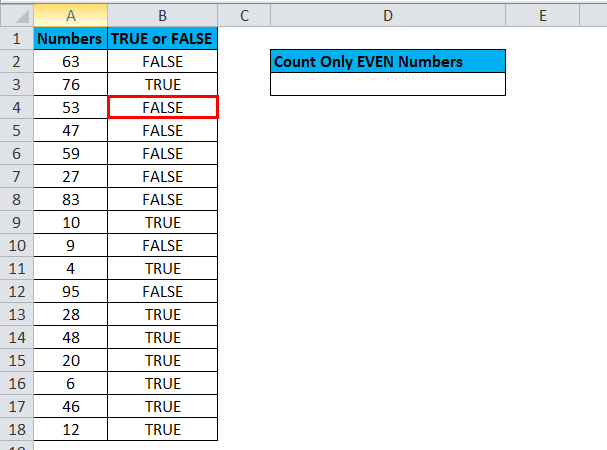
In this example, Find all the EVEN numbers from the list below and count how many there are.
We can find the total number of EVEN numbers using the EVEN and COUNTIF formulas.
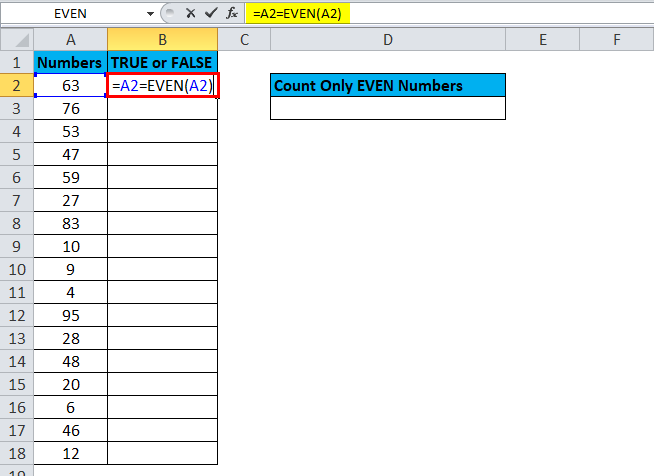
Step 1: Check each number whether it is EVEN or ODD.
Result is :
If it is, the EVEN number shows as TRUE.
If it is, the ODD number shows as FALSE.
The formula checks whether the value in cell A2 equals the closest EVEN number. If it is equal, it will return TRUE; if not, it will return FALSE.
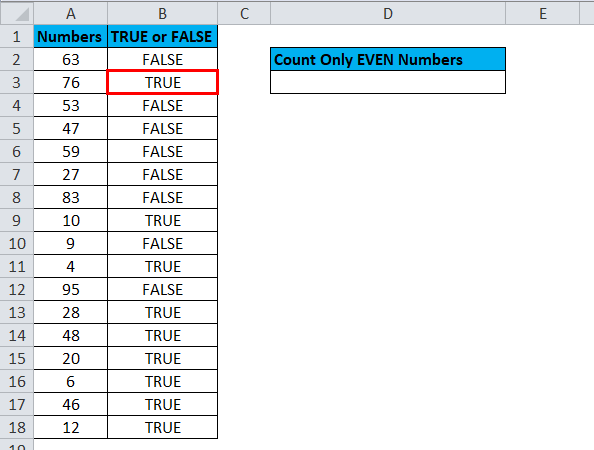
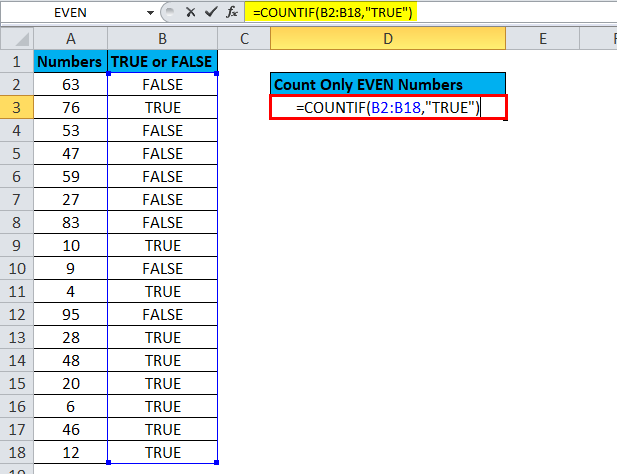
Step 2: Apply the COUNTIF formula in cell D3 to get the total count of TRUE, representing EVEN numbers in the list.
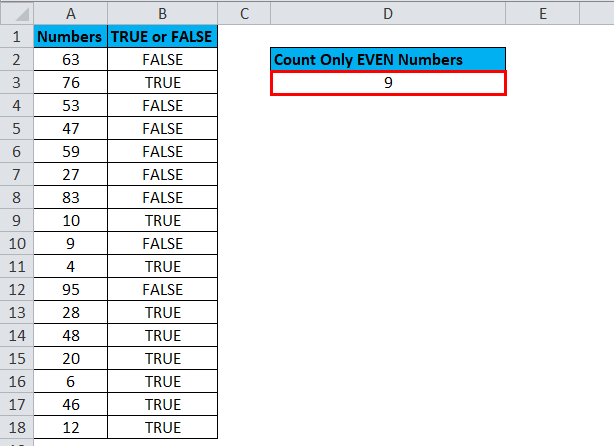
Here COUNTIF formula counts all the TRUE values in the range B2: B18 and returns the total count of all the TRUE values. The total number of TRUE values in B2: B18 is 9. That means there are 9 EVEN numbers are there in the list.
Example #3
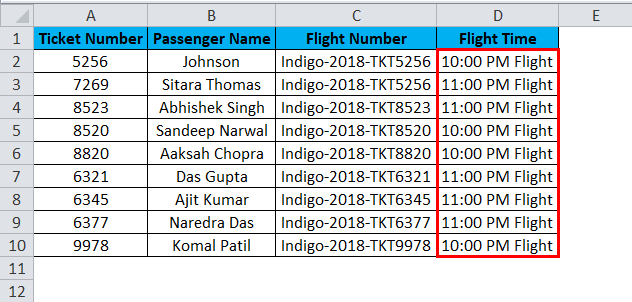
In this example, if the ticket number is an EVEN number below the passenger’s data, schedule them for a 10:00 PM flight. If the ticket number is an ODD, schedule them for the 11:00 PM flight.
Now enter this data in Excel and follow the steps below to allocate a flight to 10:00 PM or 11:00 PM.
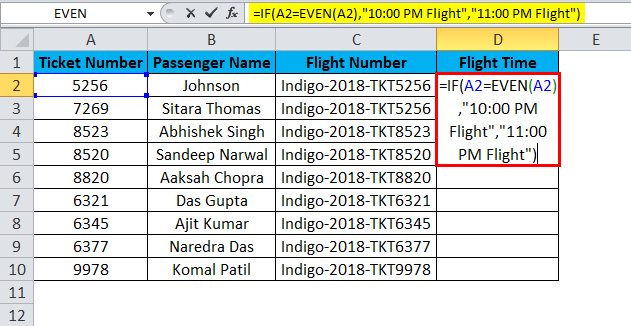
Check if the ticket number equals the EVEN number shown as “10:00 PM Flight” or “11:00 PM Flight”.
Firstly, we check whether the ticket number equals an EVEN number using the logical function IF condition. If the first supplied condition is true, the result will be shown as “10:00 PM Flight” or “11:00 PM Flight”.
EVEN Function in VBA
In VBA, also we can use the EVEN function. The procedure to use this function is as below.
Sub EVEN_Function_Example
Dim Result as String
Result = Application.Worksheetfunction.Even(51.36)
Msgbox Result
End Sub
If you run the above code message box will show you the result as 52.
Things to Remember
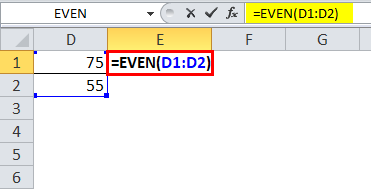
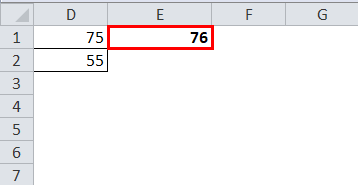
- It can be applied to a single cell, not a range of cells. If you use it for multiple cells, only the first cell will be its reference. Look at the example below; we have selected two numbers, but it shows the even number only for the number 75, and 76 is the nearest EVEN number.
Result is :
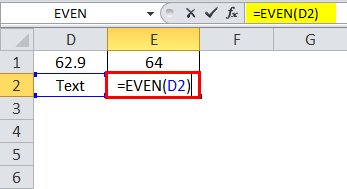
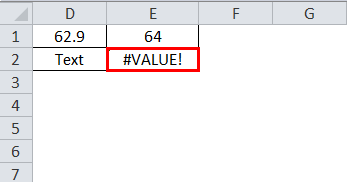
- It can be applied only to a series of numbers. If applied to something other than numbers, it will throw the error as #VALUE!
The result will be :
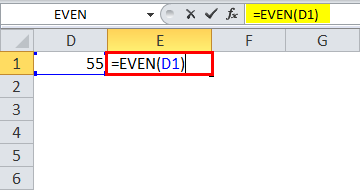
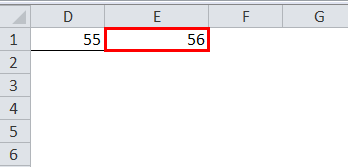
- If the number is exactly between the two EVEN numbers, a function always rounds up the number and shows the result. It will never round down the value. In the below example, the supplied number is 55.
In this case, the result will be 56, not 54.
- We can directly enter the number for the parameter and need not specify the cell reference.
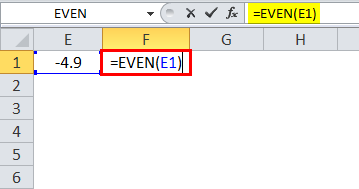
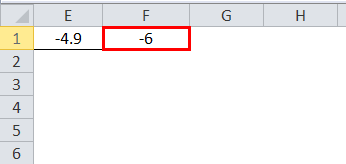
- It always rounds up for positive numbers, but it will round down for negative numbers, but the more negative it will be
Result is :
Recommended Articles
This has been a guide to EVEN Function. Here we discuss the EVEN Formula and How to use the EVEN Function, along with an example and downloadable Excel template. You may also look at these useful functions in Excel –