Updated July 26, 2023

Effective Interest Rate Formula (Table of Contents)
What is the Effective Interest Rate Formula?
The term “effective interest rate” refers to the investment’s true annual yield that is earned due to the result of compounding over the period of time.
Conversely, the effective interest rate can be seen as the true cost of borrowing from the point of view of a borrower. It is also known as the effective annual return or the annual equivalent rate. The formula for effective interest rate can be derived on the basis of the stated rate of interest and the number of compounding periods per year. Mathematically, it is represented as,
where,
- i = Stated Rate of Interest
- n = Number of Compounding Periods Per Year
Examples of Effective Interest Rate Formula (With Excel Template)
Let’s take an example to understand the calculation of Effective Interest Rate in a better manner.
Effective Interest Rate Formula– Example #1
Let us take the example of an investment with the stated rate of interest of 10%. Calculate the effective interest rate if the investment is to be compounded twice a year.

Solution:
Effective Interest Rate is calculated using the formula given below
Effective Interest Rate = (1 + i/n)n – 1
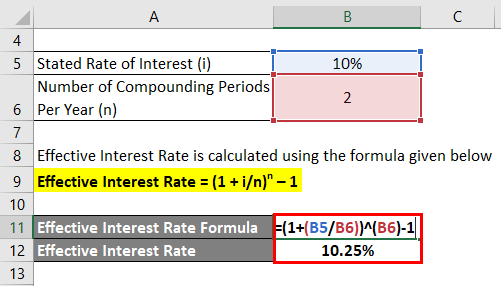
- Effective Interest Rate = (1 + 10%/2) 2 – 1
- Effective Interest Rate = 10.25%
Therefore, the effective interest rate for the quoted investment is 10.25%.
Effective Interest Rate Formula– Example #2
Let us take the example of John who is interested in investing a bond that offers a stated rate of interest of 9%. However, the nature of compounding is different and John is not sure which compounding will yield the highest return. Calculate the effective interest rate and help John take a fruitful decision for the following compounding period:
- Annual
- Half-yearly
- Quarterly
- Monthly
- Daily

Annual
Effective Interest Rate is calculated using the formula given below
Effective Interest Rate = (1 + i/n)n – 1

- Effective Interest Rate = (1 + 9%/1) 1 – 1
- Effective Interest Rate = 9%
Half-Yearly
Effective Interest Rate is calculated using the formula given below
Effective Interest Rate = (1 + i/n)n – 1
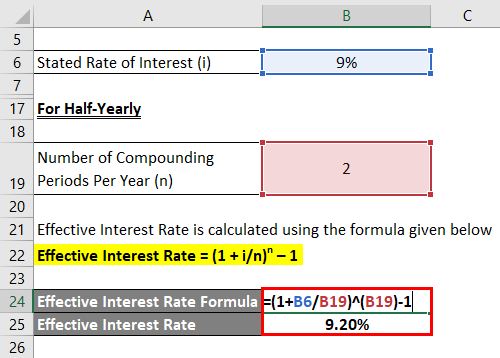
- Effective Interest Rate = (1 + 9%/2) 2 – 1
- Effective Interest Rate = 9.20%
Quarterly
Effective Interest Rate is calculated using the formula given below
Effective Interest Rate = (1 + i/n)n – 1
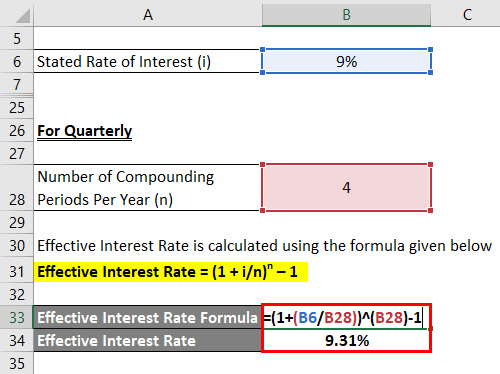
- Effective Interest Rate = (1 + 9%/4) 4 – 1
- Effective Interest Rate = 9.31%
Monthly
Effective Interest Rate is calculated using the formula given below
Effective Interest Rate = (1 + i/n)n – 1
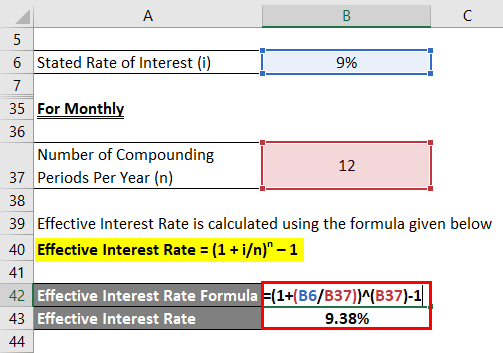
- Effective Interest Rate = (1 + 9%/12) 12 – 1
- Effective Interest Rate = 9.38%
Daily
Effective Interest Rate is calculated using the formula given below
Effective Interest Rate = (1 + i/n)n – 1
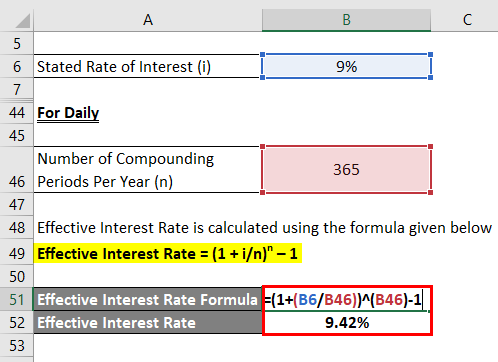
- Effective Interest Rate = (1 + 9%/365) 365 – 1
- Effective Interest Rate = 9.42%
Therefore, it can be clearly seen that annual yield increases with the increase in the number of compounding happening per year. As such, the option of daily compounding will offer the best yield for John (effective interest of 9.38% against the stated rate of interest of 9%).
Explanation
The formula for the effective interest rate can be derived by using the following steps:
Step 1: Firstly, determine the stated rate of interest of the investment, which is usually mentioned in the investment document. It is denoted by ‘i’.
Step 2: Next, figure out the number of compounding periods during a year and it is denoted by “n”. Usually, the compounding is done quarterly, half-yearly and annually which means a number of compounding per year of 4, 2 and 1 respectively.
Step 3: Finally, the formula for effective interest rate can be derived by using the stated rate of interest (step 1) and a number of compounding periods per year (step 2) as shown below.
Effective Interest Rate = (1 + i/n)n – 1
Relevance and Uses of Effective Interest Rate Formula
It is important to understand the concept of an effective interest rate because it is a vital metric for an investor or another financial user. The investors tend to use the effective interest rate predominantly as it is the actual yield received from an investment. As such, the investors lay greater emphasis on the number of compounding per year as a higher number of compounding means greater yield. On the other hand, the perspective changes for a borrower who seeks a lower number of compounding per year as it would keep their interest expense low and result in better profitability.
The concept of effective interest rate is very dependent on the number of compounding happening during a year that finally higher yield or eventually higher redemption value at maturity. Typically, the effective annual rate increases with the increase in the number of compounding per year. Although compounding can be done an infinite number of times, it should be kept in mind that there is a certain limit to the compounding effect and beyond which the phenomenon ceases to happen. That type of compounding is known as continuous compounding for which the effective interest rate is expressed as – ei, i is the stated rate of interest and it is independent of the compounding period.
Effective Interest Rate Formula Calculator
You can use the following Effective Interest Rate Formula Calculator
| i | |
| n | |
| Effective Interest Rate | |
| Effective Interest Rate = | (1 + i/n)n-1 |
| = | (1 + 0/0)0-1 = 0 |
Recommended Articles
This is a guide to the Effective Interest Rate Formula. Here we discuss how to calculate Effective Interest Rates along with practical examples. We also provide an Effective Interest Rate calculator with a downloadable Excel template. You may also look at the following articles to learn more –

