Introduction to Binary and Hexadecimal Systems
Binary and hexadecimal are fundamental number systems and the backbone of computer science and digital electronics. Based on powers of 2, Binary utilizes only two digits: 0 and 1. This simplicity makes it ideal for representing data in computing systems. After all, computers operate using electrical signals that can be either on (1) or off (0). Conversely, hexadecimal is a base-16 numerical system utilizing 16 unique symbols to denote values. The digits in hexadecimal go from 0 to 9, and then continue with letters A to F to represent values 10 to 15. Both binary and hexadecimal play crucial roles in digital computing, from representing data in memory to encoding instructions for processors. Understanding these systems is essential for anyone in computer science and engineering.
Table of Contents
- Introduction to Binary and Hexadecimal Systems
- Understanding Binary Numbers
- How to Represent Binary Numbers
- Understanding Hexadecimal Numbers
- How to Represent Hexadecimal Numbers
- Examples of Hexadecimal Numbers
- Binary to Hexadecimal Conversion Method
- Fractional Binary to Hexadecimal Direct Conversion Method
- Why convert Binary to Hexadecimal
- Practical Applications of Binary and Hexadecimal Conversion
Understanding Binary Numbers
Binary numbers consist of binary digits, often called bits, where each bit has a choice of only two values: 0 or 1. These values signify whether an electrical signal is present or absent in digital systems. Bits serve as the fundamental units for storing and processing information in computers. They form the foundation for all digital data creation and management.
| Decimal | Binary |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
How to Represent Binary Numbers
Binary numbers utilize a positional notation system akin to the decimal system. However, each digit’s position in binary signifies a power of 2 rather than 10. The rightmost digit symbolizes 2^0 (1), followed by 2^1 (2) for the next digit to the left, and 2^2 (4) for the subsequent one, and so forth. This positional system facilitates the representation of numbers of any scale using solely the digits 0 and 1. To convey a value in binary, one calculates the sum of each bit multiplied by its respective power of 2.
Example of Binary Numbers
Binary numbers can range from simple single-digit numbers, such as 0 and 1, to complex sequences of multiple digits.
For instance, the binary number 11010 represents the decimal value
(1 * 24) + (1 * 23) + (0 * 22) + (1 * 21) + (0 * 20) = 26.
| Digit | 1 | 1 | 0 | 1 | 0 |
| Binary | 24 | 23 | 22 | 21 | 20 |
| Decimal | 16 | 8 | 0 | 2 | 0 |
Similarly, binary numbers like 1001111011 represent other decimal values. Understanding binary notation is fundamental for comprehending how digital systems store and manipulate data, forming the bedrock of computer science and engineering principles.
Understanding Hexadecimal Numbers
Hexadecimal numbers operate on a base-16 numeral system. Unlike binary, which relies solely on two digits (0 and 1), hexadecimal expands its repertoire to sixteen distinct symbols: 0-9 for values 0-9 and A-F for values 10-15. In a hexadecimal number, each digit’s position aligns with a power of 16, mirroring the functionality of the decimal system with powers of 10.
| Decimal | Hexadecimal |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
How to Represent Hexadecimal Numbers
Hexadecimal numbers are often denoted with a “0x” prefix to distinguish them from decimal numbers. For example, the notation “0x2A” signifies the hexadecimal value 2A, equivalent to 42 in decimal format. This system proves useful for succinctly representing extensive binary numbers, as each hexadecimal digit represents a set of four binary digits (bits).
| Hexadecimal | Binary |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
Examples of Hexadecimal Numbers:
Low-level programming and digital electronics widely use hexadecimal numbers. They are the go-to choice for memory addresses and color codes in HTML and CSS. Mastering hexadecimal is crucial for efficiently handling binary-coded data, as it provides a more compact and readable representation than binary.
Binary to Hexadecimal Conversion Method
Method 1: Direct Conversion Method
Let us understand the direct conversion method by an example:
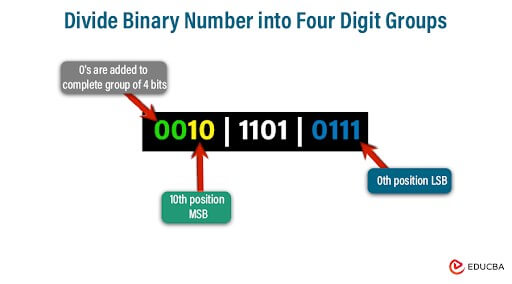
Let’s convert the binary number 1011010111 using direct method
- Dividing the Binary Number into Groups of Four Digits:
- Starting from the rightmost digit of the binary number.
- Divide it into groups of four digits.
- If the number of digits is not a multiple of four, add leading zeros to complete the last group.
Grouping: 0010|1101|0111
- Convert each group to Hexadecimal:
Convert each group of four binary digits into its corresponding hexadecimal digit using a conversion table.
Conversion:
| Binary | Hexadecimal |
| 0010 | 2 |
| 1101 | D |
| 0111 | 7 |
Binary: 0010|1101|0111
Hexadecimal: 2|D|7
- Concatenate Hexadecimal Digits
Concatenate the hexadecimal digits obtained from each group to form the final hexadecimal representation of the binary number.
After Concatenation, the digit we get is:
(1011010111)2 = (2D7)16
Method 2: Binary to Decimal to Hexadecimal Method
Let’s convert the binary number 101101110011 using the binary to decimal to hexadecimal conversion method:
- Convert Binary to Decimal:
Binary number: 101101110011
= (1*211) + (0*210) + (1*29) + (1*28) + (0*27) + (1*26) + (1*25) + (1*24) + (0*23) + (0*22) + (1*21) + (1*20)
Decimal: 2931
- Convert Decimal to Hexadecimal:
Transform the decimal number acquired in the initial step into its hexadecimal equivalent using the standard conversion method.
Decimal: 2931
| Division by 16 | Quotient | Remainder | Digit Position |
| 2931/16 | 183 | 3 | 0 |
| 183/16 | 11 | 7 | 1 |
| 11/16 | 0 | 11 | 2 |
= 11|7|3
Hexadecimal: B73
Therefore, the hexadecimal equivalent of the binary number 101101110011 is B73, obtained using the binary to decimal to hexadecimal conversion method.
Fractional Binary to Hexadecimal Direct Conversion Method
- Begin by converting the fractional binary number into its hexadecimal equivalent.
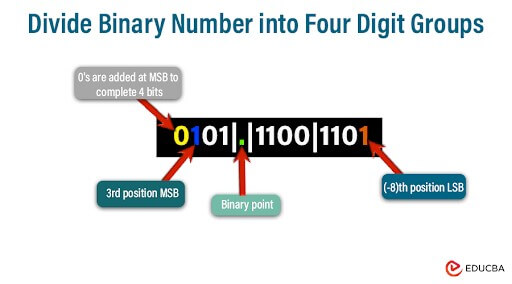
Let’s convert the fractional binary number 101.11001101 directly to hexadecimal.
- Group the binary digits after the binary point into four sets, starting from the leftmost digit. If needed, add leading zeros to complete the last group.
Grouping and Conversion: 0101|.|1100|1101
- Convert each group of four binary digits into its corresponding hexadecimal digit using a conversion table.
Binary: 0101|.|1100|1101
Hexadecimal: 5.CD
Therefore, the hexadecimal equivalent of the fractional binary number 101.11001101 is 5.CD.
Why convert Binary to Hexadecimal?
- Compactness: Hexadecimal notation offers a more concise representation of binary data compared to binary itself. Every hexadecimal digit corresponds to four binary digits (bits), significantly reducing the characters required for large binary values. This compactness streamlines data storage, transmission, and interpretation, especially for la mustbinary sequences.
- Simplified Notation: Hexadecimal notation provides a more precise and intuitive representation of binary-coded data in programming contexts. When dealing with memory addresses, machine instructions, or binary-encoded data structures, hexadecimal numbers offer a more readable and manageable format. This simplification improves code clarity, debuggability, and overall software maintainability.
- Efficient Manipulation: Converting binary numbers to hexadecimal streamlines the manipulation and processing of binary data within software applications. Hexadecimal numbers align neatly with byte boundaries commonly encountered in computer memory and data transmission. This alignment simplifies bitwise operations, data encoding, decoding, and error detection/correction algorithms, enhancing computational efficiency and algorithmic performance.
- Interoperability: Hexadecimal representation fosters interoperability across digital systems, protocols, and hardware interfaces. Many communication protocols, file formats, and device configurations rely on hexadecimal notation for specifying settings, transmitting data, or addressing memory locations. By converting binary data to hexadecimal, compatibility and seamless integration are ensured across various platforms, devices, and software environments, facilitating data exchange and system interoperability.
Practical Applications of Binary and Hexadecimal Conversion
- Programming and Software Development:
- Memory addressing frequently uses binary and hexadecimal representations, bitwise operations, and data encoding in programming.
- Binary-to-hexadecimal conversion simplifies the representation of memory addresses, machine instructions, and data structures, enhancing code readability and efficiency.
- Hexadecimal representation is often used in debugging tools and low-level programming environments to inspect memory contents and analyze program execution.
- Digital Electronics and Hardware Design:
- In digital electronics, binary and hexadecimal conversions are essential for designing digital circuits, memory mapping, and configuring hardware components.
- Binary-to-hexadecimal conversion simplifies the representation of binary-coded hardware configurations and facilitates communication between digital systems.
- Engineers use hexadecimal notation to specify register values, configure FPGA/ASIC devices, and program microcontrollers, streamlining hardware design and development processes.
- Networking and Communication Protocols:
- In networking, binary and hexadecimal conversions are integral to designing and implementing communication protocols, packet headers, and addressing schemes.
- Hexadecimal representation is commonly used in network configuration settings, IP addresses, and MAC addresses, providing a more compact and human-readable format than binary.
- Binary-to-hexadecimal conversion aids network engineers in analyzing network traffic, troubleshooting communication issues, and configuring network devices efficiently.
- Data Representation and Encoding:
- Binary and hexadecimal conversions are crucial in data representation, encoding, storing, and transmitting digital data across different platforms and systems.
- File formats often use hexadecimal notation, encoding schemes, and data serialization protocols to represent binary data concisely and facilitate data interchangeability.
- Binary-to-hexadecimal conversion is utilized in digital media formats, cryptographic algorithms, and data compression techniques to optimize data storage, transmission, and processing.
- Embedded Systems and Firmware Development:
- Binary and hexadecimal conversions are essential in embedded systems and firmware development for configuring hardware peripherals, memory mapping, and firmware programming.
- Hexadecimal notation is commonly used in register-level programming, device drivers, and firmware development environments to interact with hardware components and configure system settings.
- Binary-to-hexadecimal conversion simplifies the representation of binary-coded firmware images, bootloaders, and firmware updates, facilitating embedded systems development and deployment.
Conclusion
Binary and hexadecimal conversions are core concepts in digital technology, providing vital tools for processing and communicating data across diverse fields. Their compactness, efficiency, and readability make them indispensable in programming, electronics, networking, and data representation. Understanding these conversions grants valuable insights into digital systems, empowering individuals to design and troubleshoot technologies effectively. Proficiency in binary and hexadecimal conversions enables professionals to address programming, networking, and data analysis challenges confidently. These conversions remain essential as technology evolves, serving as the foundation for AI, cybersecurity, and IoT innovation. Mastering these skills isn’t just theoretical but practical, driving innovation and progress in the digital era.
Frequently Asked Questions (FAQs)
Q1. Can binary and hexadecimal conversions be automated in software applications?
Answer: Absolutely, software applications can automate binary and hexadecimal conversions using preexisting functions or libraries found in programming languages. Several languages, like Python, Java, C/C++, and JavaScript, offer built-in functions to convert binary and hexadecimal formats seamlessly. These automated conversion mechanisms are common across multiple domains, including programming, networking, digital electronics, and other fields where binary and hexadecimal representations are prevalent.
Q2. Are there any challenges associated with binary and hexadecimal conversions in practical applications?
Answer: Though binary and hexadecimal conversions are crucial in digital computing, they present challenges like precision loss, data truncation, and complexity in practical settings. Precision loss might arise during binary to decimal conversions, especially with floating-point numbers. Data truncation can occur when converting extensive binary values to hexadecimal due to memory or storage constraints. Furthermore, understanding and handling hexadecimal notation may demand specialized expertise and tools, particularly in intricate systems or environments.
Q3. Can binary and hexadecimal conversions be used in everyday life outside technical fields?
Answer: Most commonly used are binary and hexadecimal conversions in technical domains such as computer science, engineering, and telecommunications, but they also hold relevance in daily life. For instance, grasping binary and hexadecimal concepts aids in interpreting digital displays, diagnosing issues with electronic devices, and understanding the technical specifications of consumer products.
Recommended Articles
We hope that this EDUCBA information on “Convert Binary to Hexadecimal” was beneficial to you. You can view EDUCBA’s recommended articles for more information,