Updated July 24, 2023
Conditional Probability Formula (Table of Contents)
What is the Conditional Probability Formula?
The term “Conditional Probability” refers to the probability of occurrence of one (second ) event, which is dependent on the occurrence of one (first) or more other events.
The formula for conditional probability such that the probability of occurrence of (second) event A given that (first) event B has already occurred can be expressed by dividing the joint probability of events A and B by the probability of occurrence of event B. The joint probability of events A and B is the probability of both events happening simultaneously. Mathematically, conditional probability is represented as,
Formula
Where,
P(A ∩ B): Joint probability of events A and B
P(B): Probability of event B
Example of Conditional Probability Formula (With Excel Template)
Let’s take an example to understand the calculation in a better manner.
Example #1
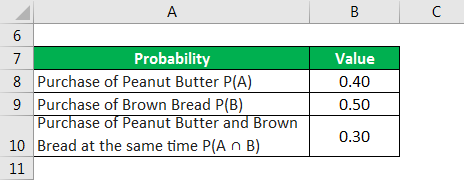
Let us take the example of a group of 100 retail buyers, out of which 50 purchased brown bread and 40 purchased peanut butter. However, 30 buyers purchased both brown bread and peanut butter. If a retail buyer selected at random purchased brown bread, what is the probability that he also purchased peanut butter? Also, determine the probability that a randomly chosen buyer has purchased brown bread, given that he also purchased peanut butter.
Solution:
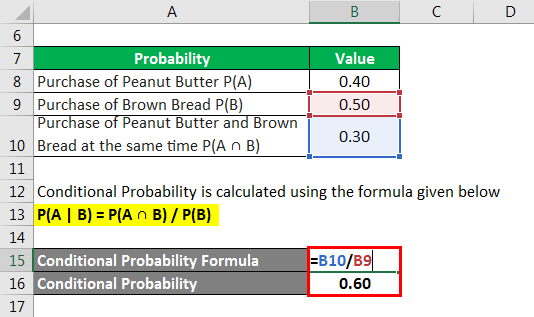
Conditional probability is calculated using the formula given below
P(A | B) = P(A ∩ B) / P(B)
- Conditional probability = 0.30 / 0.50
- Conditional Probability = 0.60
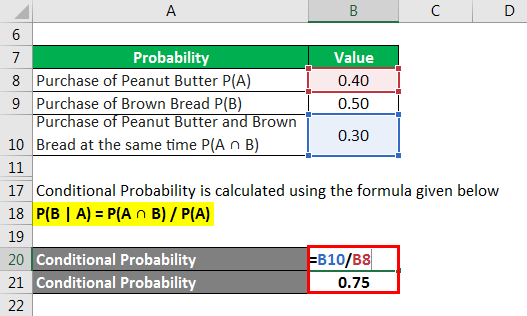
Conditional probability is calculated using the formula given below
P(B | A) = P(A ∩ B) / P(A)
- Conditional probability = 0.30 / 0.40
- Conditional Probability = 0.75
Therefore, if a buyer chosen at random is found to have purchased brown bread, then there is a 60% chance that he has also purchased peanut butter. On the other hand, if a buyer chosen at random has purchased peanut butter, then there is a 75% chance that he has also purchased brown bread.
Example #2
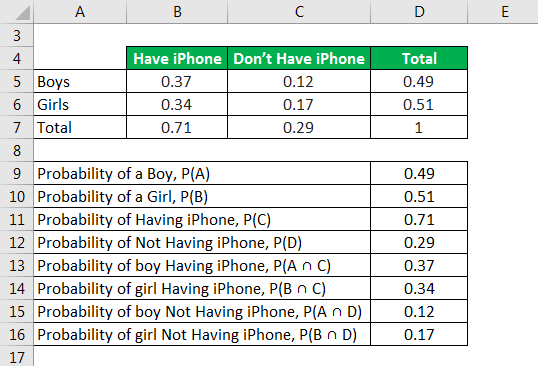
Let us now take the example of a contingency table to illustrate the concept of conditional probability. The contingency table pertains to the probability of boys and girls owning an iPhone. Calculate the following conditional probability:
- The randomly chosen person in boys that they own an iPhone.
- The randomly chosen person in girls that they own an iPhone.
- The randomly chosen person doesn’t own an iPhone, that in boys.
- The randomly chosen person doesn’t own an iPhone, that in girls.
Solution:
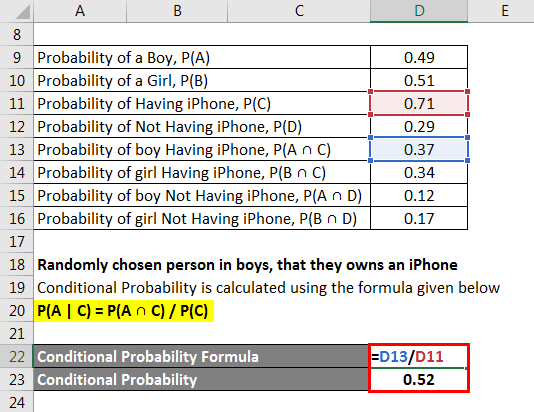
We calculate the conditional probability of boys having an iPhone using the following formula.
P(A | C) = P(A ∩ C) / P(C)
- Conditional probability = 0.37 / 0.71
- Conditional Probability = 0.52
The randomly chosen person in boys that own an iPhone = 0.52
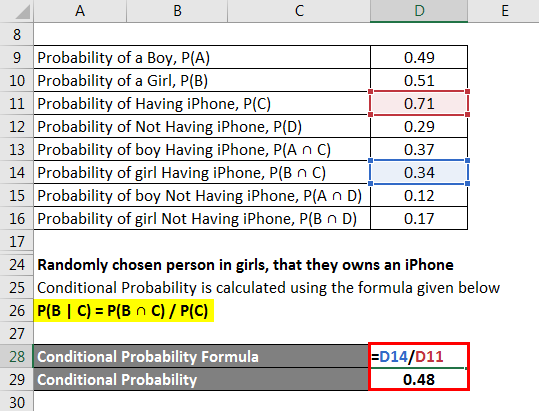
The conditional probability that girls have an iPhone is calculated using the formula given below
P(B | C) = P(B ∩ C) / P(C)
- Conditional probability = 0.34 / 0.71
- Conditional Probability = 0.48
The randomly chosen person in girls that they own an iPhone = 0.48
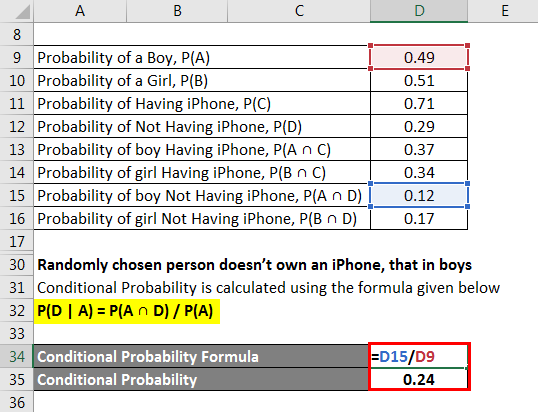
We calculate the conditional probability that boys don’t own an iPhone using the following formula
P(D | A) = P(A ∩ D) / P(A)
- Conditional probability = 0.12 / 0.49
- Conditional Probability = 0.24
The randomly chosen person doesn’t own an iPhone, that in boys = 0.24
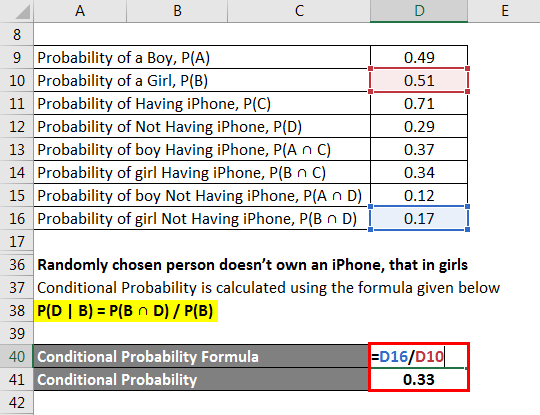
We calculate the conditional probability that girls don’t own an iPhone using the following formula
P(D | B) = P(B ∩ D) / P(B)
- Conditional probability = 0.17 / 0.51
- Conditional Probability = 0.33
The randomly chosen person doesn’t own an iPhone, that in girls = 0.33
Explanation
The Conditional Probability Formula can be computed by using the following steps:
Step 1: Firstly, determine the probability of occurrence of the first event B.
Step 2: Next, determine the probability of both events A and B happening together simultaneously. This is the joint probability of events A and B.
Step 3: We can derive the formula for the conditional probability of event A, given that event B has already occurred, by dividing the joint probability of events A and B (step 2) by the probability of event B (step 1), as shown below.
P(A | B) = P(A ∩ B) / P(B)
Relevance and Use
The concept of conditional probability is very important as it has extensive application in many areas, including finance, insurance, and politics. It states the chances of one event only when the other necessary events have already happened. However, it indicates no causal relationship between the first and second events.
Recommended Articles
This is a guide to the Conditional Probability Formula. Here we discuss how to calculate the Conditional Probability Formula along with practical examples. We also provide a downloadable excel template. You may also look aExcel following articles to learn more –