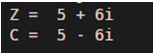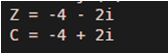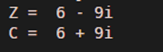Updated March 3, 2023
Introduction to Complex Conjugate Matlab
Complex conjugate for a complex number is defined as the number obtained by changing the sign of the complex part and keeping the real part the same. The significance of complex conjugate is that it provides us with a complex number of same magnitude‘complex part’ but opposite in direction. For example, if we have ‘a + ib’ as a complex number, then the conjugate of this will be ‘a – ib’. For a matrix, the complex conjugate is obtained by taking the conjugate of each element of the matrix.
In Matlab, we use ‘conj’ function for finding the complex conjugate of complex numbers.
Syntax:
C = conj (Z)
Description:
- C = conj (Z) is used to get the complex conjugate
- For a matrix, we will get a complex conjugate of every element in the input matrix
Examples of Complex Conjugate Matlab
Let us now understand the code of conj function in MATLAB using different examples:
Example #1
In this example, we will take a complex number with the positive real and imaginary parts. We will follow the following steps:
- Initialize the input complex number
- Pass this complex number as an argument to the conj function
Code:
Z = 5 + 6i
C = conj(Z)
Input:
Z = 5 + 6i
C = conj(Z)
Output:
As we can see in the output, the conjugate of 5 + 6i is 5 – 6i, which is the same as expected by us.
Example #2
In this example, we will take a complex number with the negative real and imaginary parts. We will follow the following steps:
- Initialize the input complex number
- Pass this complex number as an argument to the conj function
Code:
Z = -4-2i
C = conj (Z)
Input:
Z = -4-2i
C = conj (Z)
Output:
As we can see in the output, the conjugate of -4 – 2i is -4 + 2i, which is the same as expected by us.
Example #3
In this example, we will take a complex number with the positive real and negative imaginary part. We will follow the following steps:
- Initialize the input complex number
- Pass this complex number as an argument to the conj function
Code:
Z = 6-9i
C = conj (Z)
Input:
Z = 6-9i
C = conj (Z)
Output:
As we can see in the output, the conjugate of 6 – 9i is 6 + 9i, which is the same as expected by us. Next, let us learn how to use conj function for computing the complex conjugate of a matrix.
Example #4
In this example, we will take a 2x2matrix of complex numbers and will find the complex conjugate of the matrix. We will follow the following steps:
- Initialize the input matrix containing complex elements
- Pass this complex matrix as an argument to the conj function
Code:
Z = [3-2i1+5i; 6+2i3-2i]
C = conj (Z)
3.00 + 2.00i 1.00 – 5.00i
6.00 – 2.00i 3.00 + 2.00i]
Input:
Z = [3-2i 1+5i; 6+2i 3-2i];
C = conj (Z)
Output:
As we can see in the output, we have obtained the complex conjugate of every element of the matrix.
Example #5
In this example, we will take a 3×3 matrix of complex numbers and will find the complex conjugate of the matrix. We will follow the following steps:
- Initialize the input matrix with complex elements
- Pass this complex matrix as an argument to the conj function
Code:
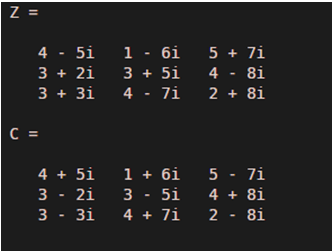
Z = [4-5i1 -6i 5 + 7i; 3+2i3 +5i 4 - 8i; 3 + 3i 4 - 7i 2 + 8i]
C = conj (Z)
4.00 + 5.00i 1.00 + 6.00i 5.00 – 7.00i
3.00 – 2.00i 3.00 – 5.00i 4.00 + 8.00i
3.00 – 3.00i 4.00 + 7.00i 2.00 – 8.00i]
Input:
Z = [4-5i 1-6i 5+7i; 3+2i 3+5i 4-8i; 3+3i 4-7i 2+8i]
C = conj(Z)
Output:
As we can see in the output, we have obtained the complex conjugate of every element of the matrix.
Conclusion
- ‘conj’ function is used in MATLAB to find the complex conjugate of complex numbers.
- It can be used to find the conjugate of complex numbers and alsoof the matrices with complex elements.
Recommended Articles
This is a guide to Complex Conjugate Matlab. Here we also discuss the introduction and syntax of complex conjugate matlab along with different examples and its code implementation. You may also have a look at the following articles to learn more –