Updated April 6, 2023

Introduction to Binary Tree Program in C
Binary tree program in C is a nonlinear data structure used for data search and organization. Binary tree is comprised of nodes, and these nodes each being a data component, have left and right child nodes. Unlike other data structures, such as, Arrays, Stack and queue, Linked List which are Linear type data structures whereas Trees are Hierarchical type of data structures. Binary search tree or BST in short, whose nodes each store keys greater than their left child nodes and less than all the right child nodes. As the data in a binary tree is organized, it allows operations like insertion, deletion, update and fetch. Let us dive deeper into the concepts related to the Binary tree and implement some of the examples using C programming language.
Syntax:
Binary tree does not have any particular Syntax but has an Algorithm to follow in implementing Binary Tree.
struct BT {
int data;
struct BT *rightNode, *leftNode;
};- Left sub tree of node contains nodes with keys less than node’s key
- Right sub tree of node contains nodes with keys greater than node’s key
- Both left and right sub tree must also be a Binary tree, and no duplicates are allowed.
Illustration of Binary Tree
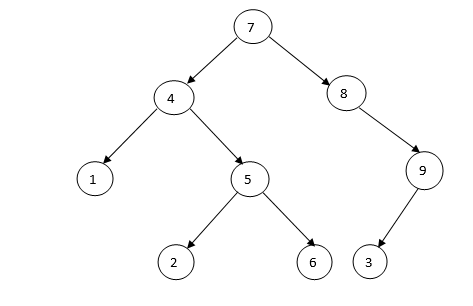
Above properties of Binary tree provide ordering among keys such that operations like search, min, and max can be done faster. If in case there is no order, then user has to compare every key for searching a given key.
Algorithm for Binary Tree:
1. A new binary tree is created and values are assigned
2. Write a function insert() in such a way that node and key will be two parameters and check for below conditions,
a. If rootNode == NULL, then return new node to calling function.
b. If rootNode => data < keyValue, then call insert() with rootNode => rightNode and assign return value in rootNode => rightNode.
c. If rootNode => data > keyValue, then call insert() with rootNode => leftNode and assign return value in rootNode => leftNode
3. Then finally, we can return original rootNode pointer to calling function.
Examples of Binary Tree Program in C
Below are the different examples of Binary Tree Program in C:
Example #1: Insertion in a Binary tree
Code:
#include<stdio.h>
#include<stdlib.h>
struct BTnode
{
int keyVal;
struct BTnode *leftNode;
struct BTnode *rightNode;
};
struct BTnode *getNode(int value)
{
struct BTnode *newNode = malloc(sizeof(struct BTnode));
newNode->keyVal = value;
newNode->leftNode = NULL;
newNode->rightNode = NULL;
return newNode;
}
struct BTnode *insert(struct BTnode *rootNode, int value)
{
if(rootNode == NULL)
return getNode(value);
if(rootNode->keyVal < value)
rootNode->rightNode = insert(rootNode->rightNode,value);
else if(rootNode->keyVal > value)
rootNode->leftNode = insert(rootNode->leftNode,value);
return rootNode;
}
void insertorder(struct BTnode *rootNode)
{
if(rootNode == NULL)
return;
insertorder(rootNode->leftNode);
printf("%d ",rootNode->keyVal);
insertorder(rootNode->rightNode);
}
int main()
{
struct BTnode *rootNode = NULL;
rootNode = insert(rootNode,7);
rootNode = insert(rootNode,4);
rootNode = insert(rootNode,8);
rootNode = insert(rootNode,1);
rootNode = insert(rootNode,5);
rootNode = insert(rootNode,2);
rootNode = insert(rootNode,9);
rootNode = insert(rootNode,3);
insertorder(rootNode);
return 0;
}Output:
![]()
So here we are creating a Binary tree and then inserting the node values.
Example #2: Binary tree, inorder, preorder, and postorder traversal
Code:
#include <stdio.h>
#include <stdlib.h>
struct BTnode {
int data;
struct BTnode* leftNode;
struct BTnode* rightNode;
};
void inorder(struct BTnode* rootNode) {
if (rootNode == NULL) return;
inorder(rootNode->leftNode);
printf("%d ->", rootNode->data);
inorder(rootNode->rightNode);
}
void preorder(struct BTnode* rootNode) {
if (rootNode == NULL) return;
printf("%d ->", rootNode->data);
preorder(rootNode->leftNode);
preorder(rootNode->rightNode);
}
void postorder(struct BTnode* rootNode) {
if (rootNode == NULL) return;
postorder(rootNode->leftNode);
postorder(rootNode->rightNode);
printf("%d ->", rootNode->data);
}
struct BTnode* createNode(value) {
struct BTnode* newNode = malloc(sizeof(struct BTnode));
newNode->data = value;
newNode->leftNode = NULL;
newNode->rightNode = NULL;
return newNode;
}
struct BTnode* insertLeftNode(struct BTnode* rootNode, int value) {
rootNode->leftNode = createNode(value);
return rootNode->leftNode;
}
struct BTnode* insertRightNode(struct BTnode* rootNode, int value) {
rootNode->rightNode = createNode(value);
return rootNode->rightNode;
}
int main() {
struct BTnode* rootNode = createNode(7);
insertLeftNode(rootNode, 4);
insertRightNode(rootNode, 8);
insertLeftNode(rootNode->leftNode, 1);
insertRightNode(rootNode->rightNode, 5);
insertLeftNode(rootNode->leftNode, 6);
insertRightNode(rootNode->rightNode, 3);
printf("Inorder \n");
inorder(rootNode);
printf("\nPreorder \n");
preorder(rootNode);
printf("\nPostorder \n");
postorder(rootNode);
}Output:
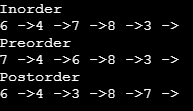
So here we have performed inorder, preorder, and postorder traversal for a Binary tree by inserting nodes.
While searching for a value in Binary Tree, node is traversed from left to right.
Types of Binary Tree
Below are the different types of binary tree:
- Full Binary Tree: Special type of Binary Tree where every parent node or an internal node has either 2 or no child nodes.
- Perfect Binary Tree: A Binary tree in which each internal node has exactly two children and all leaf nodes at same level.
- Complete Binary Tree: It is same as Full Binary Tree, but all leaf nodes must be at left and every level must have both left and right child nodes. And the last leaf node should not have the right child.
- Pathological Tree: It is the Binary Tree having a single child i.e. either left node or right node.
- Skewed Binary Tree: It is similar to a pathological tree in which the binary tree is either dominated by left or right nodes. And it has two types: Left Skewed Binary tree and Right Skewed Binary Tree.
- Balanced Binary Tree: Type of Binary Tree in which difference between the height of left and right subtree for each child node is 0 or 1
Conclusion
With this, we shall conclude our topic “Binary Tree program in C”. We have seen what Binary tree is and its Algorithm. Seen few examples on How Binary tree is created, how insertion is done, and how we can search the Binary Tree nodes and display. There are also types of Binary Tree which we have explained above. There are other operations too, which can help us to understand the concept of Binary Tree completely.
Recommended Articles
This is a guide to Binary Tree Program in C. Here we discuss the Introduction, syntax, Types of Binary Tree with Examples with code implementation. You may also have a look at the following articles to learn more –


