Updated March 13, 2023
What is Binary Search Tree in Data Structure
The binary search tree is the data structure used to maintain a sorted orderly list of elements. In this tree, each node can have a maximum of only two children. The format followed while storing the values is that the left node of the main node should have a smaller value than the main node, while the right one should have a greater value than the main node value. This pattern is followed for all the sub-nodes on the left and right sides of the main node. Subtrees of each of the individual nodes of the tree also possess both of the properties mentioned above, and hence they also act as BST, i.e., Binary Search Tree.
A particular value or number stored inside the binary tree node can be easily searched in the O (log (n)) complexity of time. This article will study the working and implementation and application of binary search trees using the C programming language.
Example of the Binary Search Tree
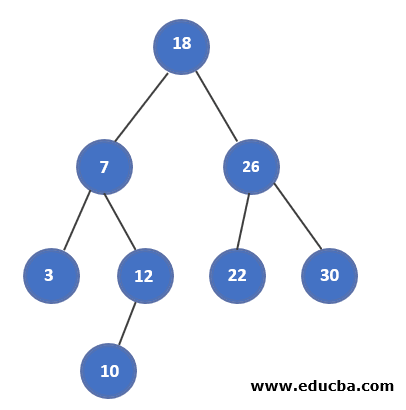
The main node should always possess a value that is greater than the left node or all of the descendants of the left node and should be smaller than the right node and all its children. The same rule applies to all of the other nodes. The following tree is the correct binary search tree example –
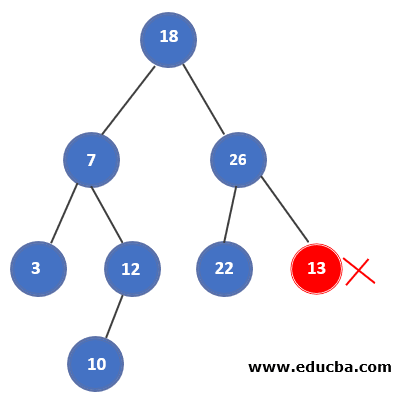
The following tree is not the proper example of the binary search tree because the node containing the value 13 should possess a value greater than 26, which is its parent or main node. Hence, the single node that follows the rules makes the below tree, not a binary search tree. Each of the nodes of the tree must follow the rules.
Implementation of the Binary Search Tree
Now, let us see how we can make use of the binary search tree data structure concept by implementing it using a C programming language. The following is the C program which contains all the proper comments explaining all the operations that are carried out, and the names of the functions are self-explanatory –
// C program for implementing the Binary search tree data structure
#include <stdio.h>
#include <stdlib.h>
struct node {
int key;
struct node *leftNode, *rightNode;
};
// Creation of the new node in the tree
struct node *newlyCreatedNode(int element) {
struct node *temporaryNode = (struct node *)malloc(sizeof(struct node));
temporaryNode->key = element;
temporaryNode->leftNode = temporaryNode->rightNode = NULL;
return temporaryNode;
}
// Traversing all the nodes in order
void traversalInOrder(struct node *mainRootNode) {
if (mainRootNode != NULL) {
// Left node traversal
traversalInOrder(mainRootNode->leftNode);
// Main Root node traversal
printf("%d -> ", mainRootNode->key);
// Right node traversal
traversalInOrder(mainRootNode->rightNode);
}
}
// Insert a new item in the binary search tree
struct node *addElement(struct node *node, int key) {
// In case if the tree seems to be empty then return a newly created node
if (node == NULL) return newlyCreatedNode(key);
// Insert a new element that is node after traversing the right side
if (key < node->key)
node->leftNode = addElement(node->leftNode, key);
else
node->rightNode = addElement(node->rightNode, key);
return node;
}
// Search for the succesor that is found by traversing inorder format
struct node *minimumValueNode(struct node *node) {
struct node *presentNode = node;
// Search the node which is present at the most left side of the tree that is left most leaf
while (presentNode && presentNode->leftNode != NULL)
presentNode = presentNode->leftNode;
return presentNode;
}
// Remove the node from the tree
struct node *removeOrDeque(struct node *mainRootNode, int key) {
// In case if the tree is completely empty then return the same main root node that is supplied
if (mainRootNode == NULL) return mainRootNode;
// Search for the node which is to be deleted
if (key < mainRootNode->key)
mainRootNode->leftNode = removeOrDeque(mainRootNode->leftNode, key);
else if (key > mainRootNode->key)
mainRootNode->rightNode = removeOrDeque(mainRootNode->rightNode, key);
else {
// In case if the current node has only one of the offspring or none of the child
if (mainRootNode->leftNode == NULL) {
struct node *temporaryNode = mainRootNode->rightNode;
free(mainRootNode);
return temporaryNode;
} else if (mainRootNode->rightNode == NULL) {
struct node *temporaryNode = mainRootNode->leftNode;
free(mainRootNode);
return temporaryNode;
}
// In case if the current node has two child nodes
struct node *temporaryNode = minimumValueNode(mainRootNode->rightNode);
// Replace the the node which is being removed or deleted in the place of successor in order
mainRootNode->key = temporaryNode->key;
// Remove the identified successor node detected in order traversal
mainRootNode->rightNode = removeOrDeque(mainRootNode->rightNode, temporaryNode->key);
}
return mainRootNode;
}
// Controller for carrying out all the operations and manipulating all the data
int main() {
struct node *mainRootNode = NULL;
mainRootNode = addElement(mainRootNode, 8);
mainRootNode = addElement(mainRootNode, 3);
mainRootNode = addElement(mainRootNode, 1);
mainRootNode = addElement(mainRootNode, 6);
mainRootNode = addElement(mainRootNode, 7);
mainRootNode = addElement(mainRootNode, 10);
mainRootNode = addElement(mainRootNode, 14);
mainRootNode = addElement(mainRootNode, 4);
printf("Traversing the tree in order: ");
traversalInOrder(mainRootNode);
printf("\n The contents of the binary tree after removing the node with value 10 \n");
mainRootNode = removeOrDeque(mainRootNode, 10);
printf("Traversing the tree in order : ");
traversalInOrder(mainRootNode);
}
The output of the above code after execution is as shown below –

Complexity
Let us discuss the time and space complexities of using the binary search tree. The space complexity of the binary search tree is O(n) while carrying out each of the operations like search, insert or delete for manipulating the nodes and contents. The time complexity in each of the cases for each of the operations is as shown in the below table –
| Operations performed | Search | Insertion | deletion |
| Complexity in Best Case Scenario | O (log n) | O (log n) | O (log n) |
| Complexity in worst Case Scenario | O (n) | O (n) | O (n) |
| Complexity in average Case Scenario | O (log n) | O (log n) | O (log n) |
Applications of a Binary Search Tree
A binary search tree is used in many algorithms and computer applications. Some of them are listed below –
- Dynamic Sorting internally makes use of a binary search tree.
- In the database, multilevel indexing is implemented by using a binary search tree.
- In the UNIX kernel, the virtual memory areas are managed by using a binary search tree.
Conclusion
A binary search tree is the data structure in which each node should have a maximum of two child nodes, and the values of all the nodes on the left should have a value that is less than the current node, while on the right should have a value greater than the current one.
Recommended Articles
This is a guide to a Binary search tree in the data structure. Here we discuss the working and implementation and application of binary search tree using the C programming language. You may also look at the following articles to learn more –

