Updated April 7, 2023
Definition of Binary Search in C
Binary Search is an important searching approach that works well in a sorted array to search an element in a sorted array. It is a simple working process used to resolve complex problems. It is highly faster than a linear search as it is based on a divide and conquer approach so helps in tracking the errors immediately and normally requires log2(N) for worst-case scenarios.
Syntax:
The Syntax structure is formatted as
Int func_name (int, int, int)
{
{
If (middle > value)
Last=middle-1;
}
If (middle < value)
{
First=middle+1;
}
}How to Perform Binary search in C?
Binary Search is performed in two manners:
1. Simple loop -an iterative approach: The code is given under the loop to iterate at times.
2. Recursive Process: The declared function in the program is called by itself.
This popular Binary search works by doing the comparison between the elements. One element is taken as a mid-element of the array and based on this the procedure is formatted. It does by minimum possible comparisons. To do this we need an array to be scanned and should be sorted in any order (descending/ascending). Means arranging the elements in a specific order. Binary search doesn’t work for unsorted array list.
To search for the respective items in ascending order the first step is the item value is compared with the middle element of the list (an entire array). If the item value is more than the middle element, the latter half of the segment becomes a new segment. If the item is less than the middle element, the first half of the segment is treated as a new segment to get through further. The same procedure is repeated until the searched item is found.
Let’s see an array example here.
The array data is given here:
Step 1: Searching an element 45. Assigning two pointers in the array list say first and last respectively. The middle element is found by the above-mentioned mathematical calculation.
Lets say first=1; last =12. The mid element is identified as mid=(1+12)/2 = 6. So the Mid element is 6 here. if suppose the value== mid, it returns the middle value.
Step 2: The Value in the 6th position is 29. And 29<45
So, first= mid+1; -> first=6+1=7 Now the first becomes ‘7’ we need to take latter half of the array list.
Step 3: mid= (7+12)/2 =9
The value is 9th position is 43. Well, 43<45 then first=mid+1; which gives first as 10.
a [6] a [7] a [8] a [9] a [10] a [11] a[12]
Step 4: Taking mid= (10+12)/2 =11
The data in the 11th position is 50. so, 50 >45.
a[9] a[10] a[11]
Then now we need to calculate by
Last= mid-1 -> last = 11-1 -> last =10. So, the item 50 is placed in the 10th position.
Step-5: mid= 10+10, as the last and first element is the same. Therefore, the mid returns 10.
The first and last position is 8. The value in the 8th position on the array is 45. Now the search is successful at location number. And the data in the 10th place is 45.
mid
Examples
The following examples are given below:
Example #1: Recursive Implementation
Code:
#include <stdio.h>
int bsearch(int narr[], int d, int b, int a)
{
if (b >= d) {
int midval = d + (b - d) / 2;
if (narr[midval] == a)
return midval;
if (narr[midval] > a)
return bsearch(narr, d, midval - 1, a);
return bsearch(narr, midval + 1, b, a);
}
return -1;
}
int main(void)
{
int narr[] = { 5, 6, 7, 20, 30 };
int s1 = sizeof(narr) / sizeof(narr[0]);
int a = 20;
int final =bsearch(narr, 0, s1 - 1, a);
(final == -1) ? printf("The element couldn’t find on the array list")
: printf("The element is found at the list %d",
final);
return 0;
}Explanation
The above C code declares a function bsearch() when the size is evaluated the items are compared with the middle position. Each time the function is called by itself to give the exact position of the number.
Output:
Example #2: Iterative loop
Code:
#include <stdio.h>
int iterationdemo(int ardata[], int first_n, int last_n, int val){
while (first_n <= last_n){
int midd_n = first_n + (last_n- first_n )/2;
if (ardata[midd_n] == val)
return midd_n;
if (ardata[midd_n] <val)
first_n = midd_n + 1;
else
last_n = midd_n - 1;
}
return -1;
}
int main(void){
int ardata[] = {11, 13, 15, 22, 24, 29,32,38,43,45,50,54};
int size = 11;
int val = 50;
int z = iterationdemo(ardata, 0, size-1, val);
if(z == -1 ) {
printf("Not found, try with some other value ");
}
else {
printf("Element found at the position : %d",z);
}
return 0;
}Explanation
This is the same as the previous program but the difference with the iteration process. While Statement is executed to find the value.
Output:
Example #3: Without using function Prototype
Code:
#include<stdio.h>
#include<conio.h>
int main()
{
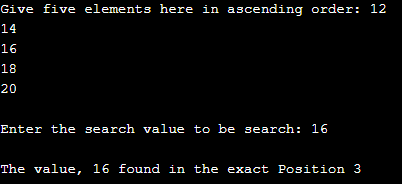
int k, ar_val[10], find, initial, final, midpos;
printf("Give five elements here in ascending order: ");
for(k=0; k<5; k++)
scanf("%d", &ar_val[k]);
printf("\nEnter the search value to be search: ");
scanf("%d", &find);
initial = 0;
final = 4;
midpos = (initial+final)/2;
while(initial <= final)
{
if(ar_val[midpos]<find)
initial = midpos+1;
else if(ar_val[midpos]==find)
{
printf("\nThe value, %d found in the exact Position %d", find, midpos+1);
break;
}
else
final = midpos-1;
midpos = (initial+final)/2;
}
if(initial>final)
printf("\nThe number, %d is not seen in a given sorted Array", find);
getch();
return 0;
}Explanation
Here the user provides input during runtime and the five numbers are entered, immediately the search process is done from the given list of the array list.
Output:
Conclusion
Therefore, in this article, we have learned how to search an element using binary search from a given sorted array. And the step-by-step demonstration is been given. It limits its works by not working on two sub-arrays and limits by search space with the pointers which is an added advantage of this search.
Recommended Articles
This is a guide to Binary Search in C. Here we discuss definition, syntax, and parameters, How to perform Binary search in C? examples with code implementation. You may also have a look at the following articles to learn more –