Updated March 14, 2023
Introduction to AVL Tree Rotation
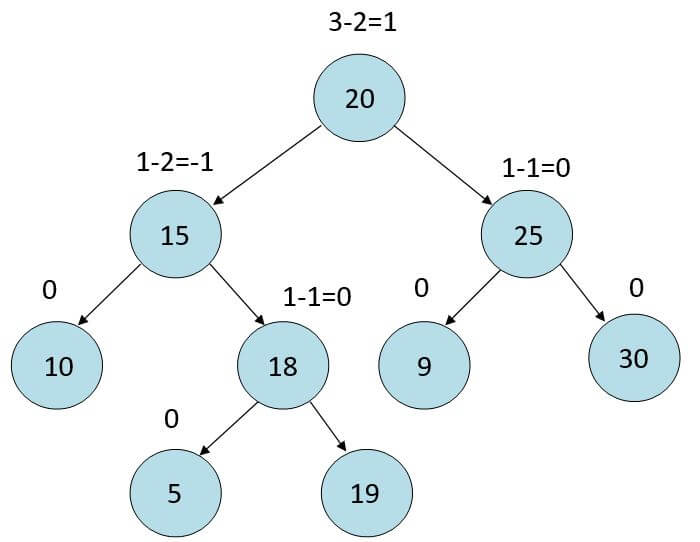
The following article provides an outline for AVL Tree Rotation. AVL Tree is a Binary Search Tree and is also known as a self-balancing tree in which each node is connected to a balance factor which is calculated by subtracting the heights of the right subtree from that of the left subtree of a particular node. The tree is defined as a balanced AVL tree when the balance factor of each node is between -1 and 1. On the other hand, when the balance factor is less than -1 or greater than 1, then the tree is known as an unbalanced tree and needs to be balanced to get the perfect AVL tree.
- If the balance factor obtained is -1 for a particular node, it defines that the node’s left subtree is one level higher than the right subtree.
- If the balance factor obtained is 0 for a particular node, it defines that the node’s left subtree and right subtree are at an equal level.
- If the balance factor obtained is 1 for a particular node, it defines that the left subtree is one level lower than the node’s right subtree.
Balanced AVL Tree Example:
Rotation Operations in AVL Tree
Rotation is performed in AVL Tree to turn the unbalanced tree into a balanced tree by performing various rotation operations.
In general, there are four types of Rotations in the AVL tree:
- Left Rotation
- Right Rotation
- Left-Right Rotation
- Right-Left Rotation
The first two rotations are known as single rotations, and the next two are known as double rotations.
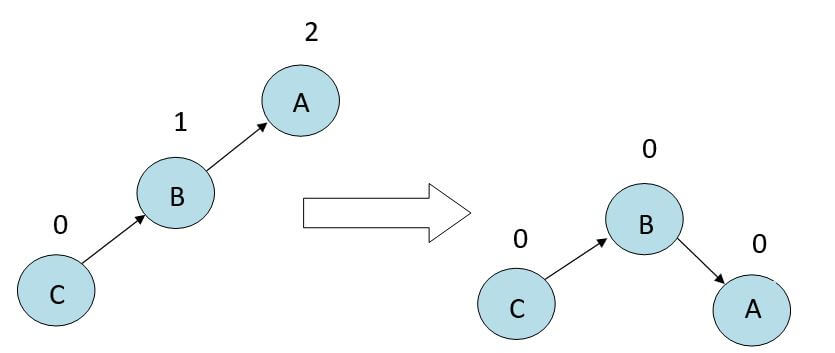
1. Left Rotation (LL)
When a node is inserted into the left subtree or deleted from the left subtree, the AVL tree becomes unbalanced, and we need to balance it using LL rotation. This LL rotation is also known as clockwise rotation applied on edge, which has the highest balance factor.
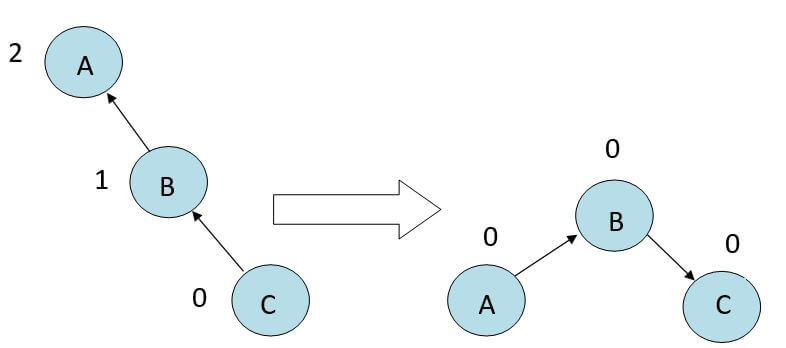
2. Right Rotation(RR)
When a node gets inserted into the right subtree or deleted from the right subtree, the AVL tree becomes unbalanced, and we need to balance it by rotating the node in the anti-clockwise direction. This rotation technique is applied on the edge of the node which is having the highest balance factor.
3. Left-Right Rotation(LR)
Left-Right Rotation is the combination of RR rotation and LL rotation. At first, RR rotation is performed on the subtree then, LL rotation is performed on the part of the full tree from inserted node to the first node
4. Right-Left Rotation(RL)
Right-left Rotation is the combination of LL rotation and RR rotation. In this case, the first LL rotation is performed on the subtree where the change has been made; then, the RR rotation is performed on the part of the full tree from the inserted node to the top of the tree, that is, the first node.
Example of AVL Tree Rotation
Given below is the example of AVL Tree Rotation:
AVL tree in Python.
Code:
import sys
# Create a node
class TreeNode(object):
def __init__(self, key):
self.key = key
self.left = None
self.right = None
self.height = 1
class AVLTree(object):
# Function to insert a node
def insert_node(self, root, key):
# Insert the node at the correct location
if not root:
return TreeNode(key)
elif key < root.key:
root.left = self.insert_node(root.left, key)
else:
root.right = self.insert_node(root.right, key)
root.height = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
# Balance the tree by updating the balance factor
balanceFactor = self.getBalance(root)
if balanceFactor > 1:
if key < root.left.key:
return self.rightRotate(root)
else:
root.left = self.leftRotate(root.left)
return self.rightRotate(root)
if balanceFactor < -1:
if key > root.right.key:
return self.leftRotate(root)
else:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
#Function to delete a node
def delete_node(self, root, key):
# Remove the deleted node
if not root:
return root
elif key < root.key:
root.left = self.delete_node(root.left, key)
elif key > root.key:
root.right = self.delete_node(root.right, key)
else:
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp=root.left
root = None
return temp
temp = self.getMinValueNode(root.right)
root.key = temp.key
root.right = self.delete_node(root.right,
temp.key)
if root is None:
return root
# Update the nodes balance factor
root.height = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
balanceFactor = self.getBalance(root)
# Balance the tree
if balanceFactor > 1:
if self.getBalance(root.left) >= 0:
return self.rightRotate(root)
else:
root.left = self.leftRotate(root.left)
return self.rightRotate(root)
if balanceFactor < -1:
if self.getBalance(root.right) <= 0:
return self.leftRotate(root)
else:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
# Function to perform tree’s left rotation
def leftRotate(self, z):
y = z.right
T2 = y.left
y.left = z
z.right = T2
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
# Function to perform tree’s right rotation
def rightRotate(self, z):
y = z.left
T3 = y.right
y.right = z
z.left = T3
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
# Get the height of the node
def getHeight(self, root):
if not root:
return 0
return root.height
# Get the node balance factor
def getBalance(self, root):
if not root:
return 0
return self.getHeight(root.left) - self.getHeight(root.right)
def getMinValueNode(self, root):
if root is None or root.left is None:
return root
return self.getMinValueNode(root.left)
def preOrder(self, root):
if not root:
return
print("{0} ".format(root.key), end="")
self.preOrder(root.left)
self.preOrder(root.right)
# Print the AVL tree
def printHelper(self, currPtr, indent, last):
if currPtr != None:
sys.stdout.write(indent)
if last:
sys.stdout.write("R----")
indent += " "
else:
sys.stdout.write("L----")
indent += "| "
print(currPtr.key)
self.printHelper(currPtr.left, indent, False)
self.printHelper(currPtr.right, indent, True)
myTree = AVLTree()
root = None
nums = [33, 13, 52, 9, 21, 61, 8, 11]
for num in nums:
root = myTree.insert_node(root, num)
myTree.printHelper(root, "", True)
key = 13
root = myTree.delete_node(root, key)
print("After Deletion: ")
myTree.printHelper(root, "", True)
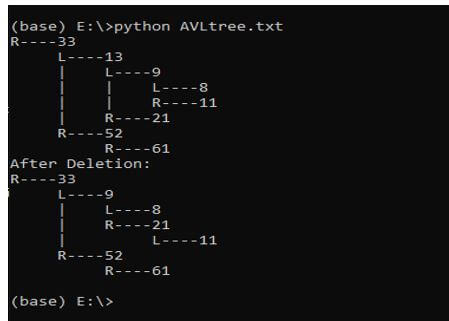
Output:
Conclusion
AVL tree is a self-balancing binary tree in which each node is connected to a balance factor. This tree is named in honor of the inventors GM Adelson-Velsky and EM Landis in 1962. The balance factor is calculated by subtracting the heights of the right subtree from the left subtree of a particular node. There are four types of Rotations in the AVL tree: Left rotation, Right rotation, Left-Right rotation, Right-Left rotation.
Recommended Articles
This is a guide to AVL Tree Rotation. Here we discuss the introduction, rotation operations in AVL tree and example, respectively. You may also have a look at the following articles to learn more –