Updated July 24, 2023
Amortized Loan Formula (Table of Contents)
What is the Amortized Loan Formula?
The term “Amortized Loan” refers to the type of loan with a well-defined periodic payment schedule for both principal and interest. In such loans, the total periodic payment obligation is equal, while the mix of interest and principal changes over the tenure of the repayment.
Initially, interest payment forms a larger portion of the periodic payment and by the end of the scheduled principal repayment becomes the major portion.
The formula of amortized loan is expressed in terms of total repayment obligation using total outstanding loan amount, interest rate, and loan tenure in terms of no. of years and no. of compounding per year. Mathematically, it is represented as,
Where,
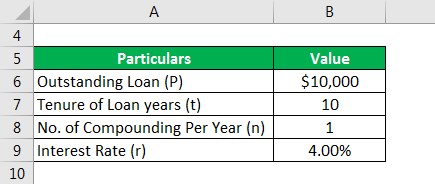
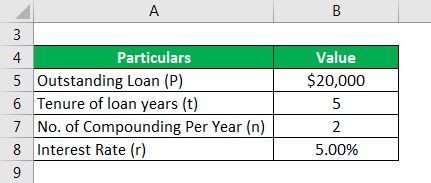
- P: Outstanding Loan Amount
- r: Interest Rate
- t: Loan Tenure in No. of Years
- n: No. of Compounding Per Year
The interest component of the total payment can be expressed as,
The principal component of the total payment can be expressed as,
Example of Amortized Loan Formula (With Excel Template)
Let’s take an example to understand the Amortized Loan calculation better.
Amortized Loan Formula – Example #1
Let us take the example of a term loan with an outstanding amount of $10,000 of loan that has to be repaid over the next 10 years. The amortization of the loan will be in the form of equated annual repayment, and the interest rate is 4%. Calculate principal repayment, interest paid, and total repayment during the first year of the loan on the basis of the given information.
Solution:
Principal Repayment is calculated using the formula given below
Principal Repayment = P * (r/n) * (1 + r/n)t*n / [(1 + r/n)t*n – 1] – P * (r/n)
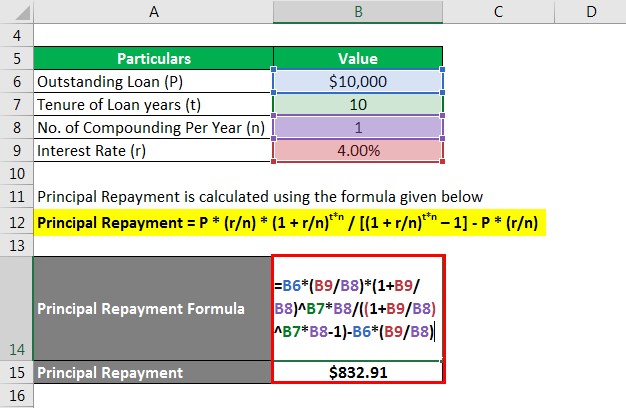
- Principal Repayment = $10,000 * (4%/1) * (1 + 4%/1)10*1 / [(1 + 4%/1)10*1 – 1] – $10,000 * (4%/1)
- Principal Repayment = $832.91
Interest Paid is calculated using the formula given below
Interest Paid = P * (r/n)
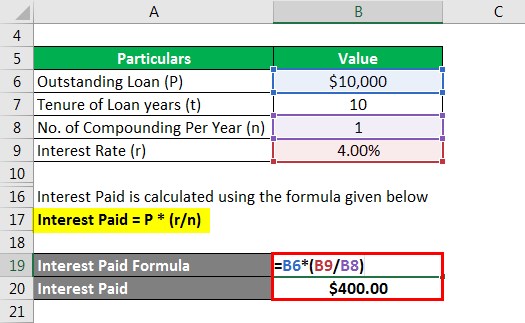
- Interest Paid = $10,000 * (4%/1)
- Interest Paid = $400.00
Total Repayment is calculated using the formula given below
Total Repayment = P * (r/n) * (1 + r/n)t*n / [(1 + r/n)t*n – 1]
- Total Repayment = $10,000 * (4%/1) * (1 + 4%/1)10*1 / [(1 + 4%/1)10*1 – 1]
- Total Repayment = $1,232.91
Therefore, the principal repayment, interest payment, and total repayment during the first year are $832.91, $400.00, and $1,232.91, respectively.
Amortized Loan Formula – Example #2
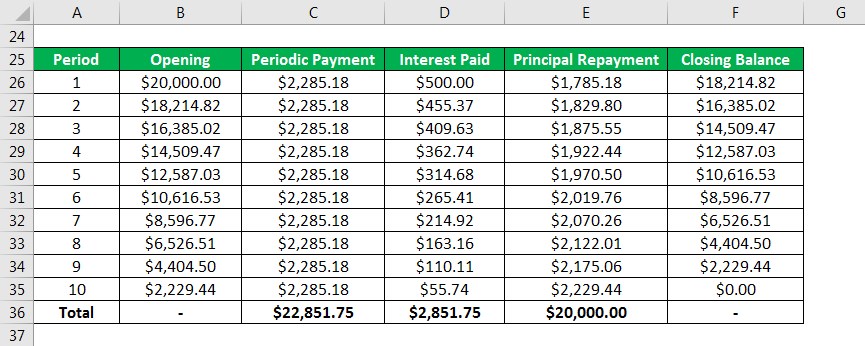
Let us take the example of a 5-year term loan with an outstanding amount of $20,000, semi-annual compounding, and an interest rate of 5%. Build the amortization schedule based on the given information.
Solution:
Principal Repayment is calculated using the formula given below
Principal Repayment = P1 * (r/n) * (1 + r/n)t*n / [(1 + r/n)t*n – 1] – P1 * (r/n)
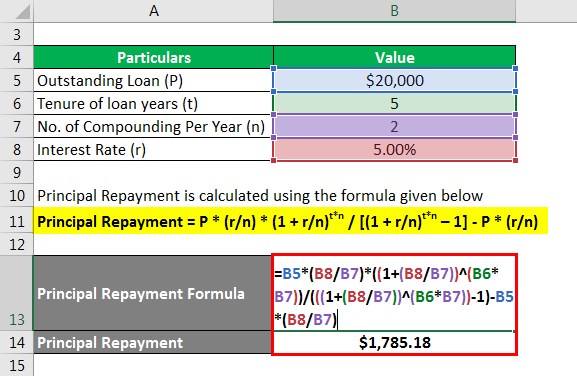
- Principal Repayment = $20,000 * (5%/2) * (1 + 5%/2)5*2 / [(1 + 5%/2)5*2 – 1] – $20,000 * (5%/2)
- Principal Repayment = $1,785.18
Interest Paid is calculated using the formula given below
Interest Paid = P1 * (r/n)
- Interest Paid = $20,000 * (5%/2)
- Interest Paid = $500.00
Total Repayment is calculated using the formula given below
Total Repayment = P1 * (r/n) * (1 + r/n)t*n / [(1 + r/n)t*n – 1]
- Total Repayment = $20,000 * (5%/2) * (1 + 5%/2)5*2 / [(1 + 5%/2)5*2 – 1]
- Total Repayment = $2,285.18
To calculate the remaining part of the Amortized, refer to the given excel template.
P2 is calculated using the formula given below.
P2 = P1 – Principal Repayment for the first 6 months
- P2 = $20,000 – $1,785.18
- P2 = $18,214.82
Principal Repayment is calculated using the formula given below
Principal Repayment = P2 * (r/n) * (1 + r/n)t*n / [(1 + r/n)t*n – 1] – P2 * (r/n)
- Principal Repayment = $18,214.82 * (5%/2) * (1 + 5%/2)5*2 / [(1 + 5%/2)5*2 – 1] – $18,214.82 * (5%/2)
- Principal Repayment = $1,829.80
Interest Paid is calculated using the formula given below
Interest Paid = P1 * (r/n)
- Interest Paid = $18,214.82 * (5%/2)
- Interest Paid = $455.37
Total Repayment is calculated using the formula given below
Total Repayment = P2 * (r/n) * (1 + r/n)t*n / [(1 + r/n)t*n – 1]
- Total Repayment = $18,214.82 * (5%/2) * (1 + 5%/2)5*2 / [(1 + 5%/2)5*2 – 1]
- Total Repayment = $2,081.20
Explanation
The formula for Amortized Loan can be calculated by using the following steps:
Step 1: Firstly, determine the loan’s current outstanding amount, denoted by P.
Step 2: Next, figure out the rate of interest to be paid on the loan, denoted by r.
Step 3: Next, determine the loan tenure in terms of no. of years, denoted by t.
Step 4: Next, figure out the no. of compounding per year for the loan, denoted by n.
Step 5: Next, compute the loan’s principal repayment for the period by using the outstanding loan amount (step 1), rate of interest (step 2), loan tenure (step 3), and no. of compounding per year (step 4).
Principal Repayment = P * (r/n) * (1 + r/n)t*n / [(1 + r/n)t*n – 1] – P * (r/n)
Step 6: Next, compute the interest to be paid for the period by multiplying the outstanding loan amount (step 1) and rate of interest (step 2) divided by the no. of compounding per year (step 4).
Interest Payment = P * (r/n)
Step 7: Finally, the formula for an amortized loan or the total repayment for the period is the aggregate of the principal repayment and the interest payment, as shown below.
Total Repayment = Principal Repayment + Interest Payment
- Total Repayment = P * (r/n) * (1 + r/n)t*n / [(1 + r/n)t*n – 1] – P * (r/n)P * (r/n)
- Total Repayment = P * (r/n) * (1 + r/n)t*n / [(1 + r/n)t*n – 1]
Relevance and Use of Amortized Loan Formula
The concept of amortized loan is fundamental to understand because it helps assess how much of the total repayment is being paid in the form of interest and what portion is principal repayment. In other words, you can easily compute the amount of money paid in interest and principal over the tenure of the loan by using the amortized loan formula. Nowadays, most loans are amortized loans (such as personal loans, home loans, auto loans, etc.) wherein the equated amount of payment is made over an extended period of time, 5 years to 30 years.
Amortized Loan Formula Calculator
You can use the following Amortized Loan Formula Calculator
| P | |
| r | |
| n | |
| t | |
| Principal Repayment | |
| Principal Repayment = | P * (r/n) * (1 + r/n)t*n / [(1 + r/n)t*n-1]-P(r/n) | |
| 0 * ( 0/0) * (1 + 0/0)0*0 / [(1 + 0/0)0*0-1] = | 0 |
Recommended Articles
This is a guide to Amortized Loan Formula. Here we discuss how to calculate the Amortized Loan along with practical examples. We also provide an Amortized Loan calculator with a downloadable excel template. You may also look at the following articles to learn more –
