Introduction to Recursion in Java
Recursion in Java is defined as “a method calls itself (same method) continuously directly or indirectly.” A recursion function is used in situations where the same set of operations needs to be performed again and again till the result is reached. It performs several iterations, and the problem statement keeps becoming simpler with each iteration. Recursion in java is a method for solving the problem based on the solution to the smaller block of the same problem. Most of the infinite possibility iterations can be solved by Recursion. We can say Recursion is an alternative way to looping statements. If we did not use the recursive function properly, then it executes infinite times.
Syntax:
returntype methodName()
{
//logic for application
methodName();//recursive call
}How Can We Stop Infinite Conditions of Recursion in Java?
To stop the infinite conditions, we must have the following:
- Base Condition: Specify inside if the condition were to stop the recursion function.
- Recursion Call: Proper recursion call.
We can call a recursion function in 2 ways:
1. Direct Recursion Call
If we call the same method from the inside method body.
Syntax:
returntype methodName()
{
//logic for application
methodName();//recursive call
}Example:
Factorial of a number is an example of direct recursion. The basic principle of recursion is to solve a complex problem by splitting it into smaller ones. For example, in the case of the factorial of a number, we calculate the factorial of “i” if we know its factorial of “i-1”.
Code:
public class Factorial {
static int fact(int i){
if (i == 1)
return 1;
else
return(i * fact(i-1));
}
public static void main(String[] args) {
System.out.println("The factorial of given number 6 is: "+fact(6));
}
}Output:
2. Indirect/Mutual Recursion Call
If we call a method from another method and another method called from the first method, vice versa.
Syntax:
<firstIndirectRecursive()
{
// Logic
secondIndirectRecursive();
}
secondIndirectRecursive()
{
//Logic
firstIndirectRecursive();
}Example:
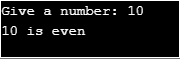
To show indirect recursion, we take the following program used to find out if a given number is even or odd from the given input.
Code:
import java.util.Scanner;
public class IndirectRecursion {
public static boolean oddNum(int i) {
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0){
return false;
} else {
return evenNum(i-1);
}
}
public static boolean evenNum(int i) {
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0){
return true;
} else {
return oddNum(i-1);
}
}
public static void main(String[] args) {
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
}
}Output:
Examples of Recursion in Java
Here are some more examples to solve the problems using the recursion method.
Example #1 – Fibonacci Sequence
A set of “n” numbers is said to be in a Fibonacci sequence if number3=number1+number2, i.e. each number is a sum of its preceding two numbers. Hence the sequence always starts with the first two digits like 0 and 1. The third digit is a sum of 0 and 1 resulting in 1, the fourth number is the addition of 1 and 1 resulting in 2, and the sequence goes on.
Check out the following code in Java to generate a Fibonacci sequence:
Code:
public class FibonacciSeries{
static int num1=0,num2=1,num3=0;
static void fibonacci(int n){
if(n>0){
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
}
}
public static void main(String args[]){
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
}
}Output:
Here the first two numbers are initialized to 0 and 1 and printed. The variables “num1”, “num2”, and “num3” is used to generate the required sequence. Variable “num3” is got by adding “num1” and “num2”, and the numbers are shifted one position to the left by shuffling as shown in the code. The function “Fibonacci” is recursively called here, and at each iteration, the value of “n” is decreased by 1. Hence the recursion exits as soon as “n” reaches value 0.
Example #2 – Tower Of Hanoi
This is a classic mathematical problem which is having 3 poles and an “n” number of disks with different sizes. The puzzle goes as follows:
In the beginning, the first pole will be having the disks arranged such that the biggest disc of them all is at the bottom and the smallest one at the top of the pole. The objective is to move these disks from the first pole to the third pole keeping the disks in the same position as that in the first. Following are a few conditions to keep in mind while shifting these disks:
- At a time, only one disk has to be moved.
- In the process, placing a larger disk over a smaller one is not allowed.
- The second (middle) pole can be used to mediate while transferring the discs from the first to the second pole.
Following is the Java code which can be used to solve the puzzle:
Code:
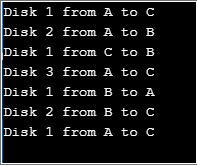
public class TowerOfHanoi {
public static void main(String[] args) {
int count = 3;
tower(count, 'A', 'B', 'C');
}
public static void tower(int first, char disk1, char temp, char disk2) {
if (first == 1) {
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
} else {
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
}
}
}Output:
Here the variable “count” represents the number of discs to be used. The function “tower” is the recursive function used to move the discs from rod 1 to rod 3. A simple solution to this problem can be provided by considering 2 discs at first.
- First, we start by moving disc1 from rod 1 to rod 2.
- Next, we move disc2 to rod 3.
- Finally, we finish by moving disc1 to rod 3, completing the required solution.
This same principle is applied for the “n” number of discs by moving (n-1)the disc from rod 1 to 2 and following similar steps as above.
Example #3 – Factorial of Number
Code:
package com.recursion;
import java.util.Scanner;
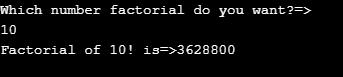
public class FactorialOfNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Which number factorial do you want?=>");
//taking input from the user
int input = scanner.nextInt();
System.out.println("Factorial of " + input + "! is=>"+getMyFactorialNumber(input));
scanner.close();
}
public static long getMyFactorialNumber(int inputNumber) {
if (inputNumber == 1)//base condition
return 1;
return inputNumber * getMyFactorialNumber(inputNumber - 1);//recursive call
}
}Output:
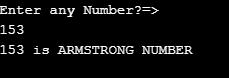
Example #4 – Armstrong Number
Code:
import java.util.Scanner;
//ARMSTRONG number means sum of numbers of cubes equal to the number
public class ArmstrongNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter any Number?=>");
// taking input from the user
int input = scanner.nextInt();
//calling isArmstrongNumber() method and put in a variable
double checkNumber=isArmstrongNumber(input);
//checking the number
if(input==checkNumber)
{
System.out.println(input+" is ARMSTRONG NUMBER");
}
else
{
System.out.println(input+" not is ARMSTRONG NUMBER");
}
scanner.close();
}
static int remainderNumber;
static double total = 0;
public static double isArmstrongNumber(int inputNumber) {
if (inputNumber > 0) {
remainderNumber = inputNumber % 10;//separating digits
total = total + Math.pow(remainderNumber, 3);//cubes sum
isArmstrongNumber(inputNumber / 10);//recursive call
}
return total;
}
}Output:
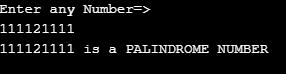
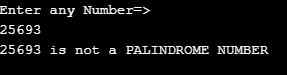
Example #5 – Palindrome Number
Code:
import java.util.Scanner;
public class PalindromeNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter any Number=>");
// taking input from the user
int input = scanner.nextInt();
int checkNumber = palindromeNumberOrNot(input,0);
if (checkNumber == input)
{
System.out.println(input+" is a PALINDROME NUMBER");
}
else
{
System.out.println(input+" is not a PALINDROME NUMBER");
}
scanner.close();
}
public static int palindromeNumberOrNot(int inputNumber,int baseNumber) {
if (inputNumber == 0)// base case
return baseNumber;
baseNumber = (baseNumber * 10) + (inputNumber % 10);// getting the reverse of the number and stores in temp
return palindromeNumberOrNot(inputNumber/10,baseNumber);//recursive call
}
}Output:
Conclusion
Recursive functions are relatively simpler to code, but they are also not that efficient as compared to the other existing methods. Hence they are majorly used in cases where the time given for development is less and also where a significant pattern can be observed in the problem.
Recommended Articles
This is a guide to Recursion in Java. Here we discuss the Introduction and how we can stop infinite conditions of Recursion in Java along with different examples and code Implementation. You may also look at the following articles to learn more-