Updated March 14, 2023
Introduction to Postorder Traversal
Postorder traversal of Binary tree is a traversal method, where left subtree is visited first, then right subtree, and finally root node. Unlike array and linked lists, being linear data structures, we have several ways of traversing binary trees due to their hierarchical nature. These tree traversal algorithms are divided into two types, i.e., Depth First Algorithms and Breadth-First Algorithms. In-Depth First Algorithm, trees are traversed downwards. On the other hand, preOrder, InOrder, PostOrder are actually depth-first traversal algorithms. PostOrder traversal is used to delete the binary tree. Let us dig deeper into the PostOrder traversal of a Binary tree and see how to preorder traversal is implemented and so on.
How PostOrder traversal of the Binary tree works?
- In preorder traversal, the left subtree is visited first, then the right subtree, and finally the root node.
- Unlike other data structures, such as Array, Queue, Stack, etc., which have only one way of traversal, but trees have 3 ways of traversal, i.e., InOrder, PreOrder, and traversals.
- Let us consider an example of a Binary tree for PostOrder traversing.
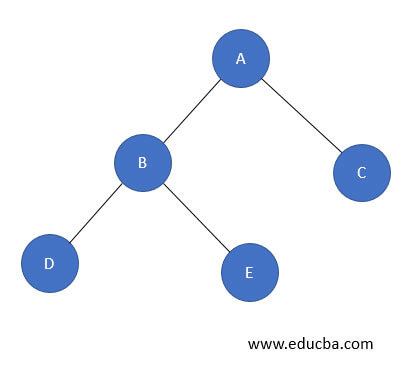
- We shall perform Depth First Traversal on the above Binary tree; Depth First consists of PreOrder, InOrder, and PostOrder; we shall see PostOrder traversing here.
- PostOrder( Left Subtree, Right Subtree, Root node ): D E B C A
- The steps followed to get PostOrder is simple, Visit the left subtree first, i.e., D, then traverse to the right subtree, i.e., E, then root node B, traverse to the right subtree, i.e., C, and then the root node for this subtree, i.e., A.
- And hence Postorder traversal will move as [D, E, B, C, A]
Algorithm for PostOrder traversal implementation
Step 1: Traverse the left subtree, i.e., traverse recursively.
Step 2: Traverse the right subtree, i.e., traverse recursively.
Step 3: Finally, visit the root node.
PostOrder traversal is useful to get the postfix of an expression in a Binary tree. In this traversal, the root node is visited at last and hence the name.
Let us see one more Binary tree for implementing Traversal,
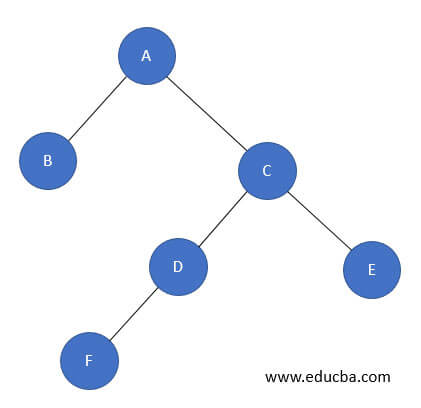
PostOrder Traversal: B F D E C A
The first element printed is B, as it is the left node.
Then traverses to the right subtree, which has left and right node, Node D has left node, i.e., F.
As there is no right node, it will traverse back to the root node of the subtree, i.e., D.
As there is no right node, it will traverse back to the root node of the subtree, i.e., C and checks if there is any right node, i.e., E.
Then traverses to the root node of the subtree, i.e., C., and then A, the main root node.
Advantages and disadvantages of Postorder traversal
Below are some advantages and disadvantages of Postorder traversal:
Advantages
- PostOrder traversal is used to delete the binary tree.
- Traversal should be used while getting postfix expression of a binary tree
- Binary tree traversals give quick searching, insertion, and deletion in cases where the tree is balanced.
- The root node value is printed at last in traversal only after visiting the left subtree and right subtree.
- It is also part of the Depth-First Algorithm, and order is left subtree > right subtree > root node.
- Traversal, part of the Depth-first algorithm, will use less memory space as compared to the Breadth-first algorithm.
Disadvantages
- Deletion algorithm in traversal in complex comparatively
- There is no possibility to get the shortest path while traversing.
- PostOrder traversal works well while traversing trees. However, as it is a depth-first algorithm, searching graphs can get you stuck in an infinite loop as depth-first algorithms travel around cyclically for graphs forever.
Example: PostOrder Traversal in Python Language.
class BinaryNode:
def __init__(self, key):
self.leftNode = None
self.rightNode = None
self.value = key
def postOrder(rootnode):
if rootnode:
postOrder(rootnode.leftNode)
postOrder(rootnode.rightNode)
print(rootnode.value),
rootnode = BinaryNode(6)
rootnode.leftNode = BinaryNode(1)
rootnode.rightNode = BinaryNode(4)
rootnode.leftNode.leftNode = BinaryNode(2)
rootnode.leftNode.rightNode = BinaryNode(3)
rootnode.leftNode.rightNode = BinaryNode(5)
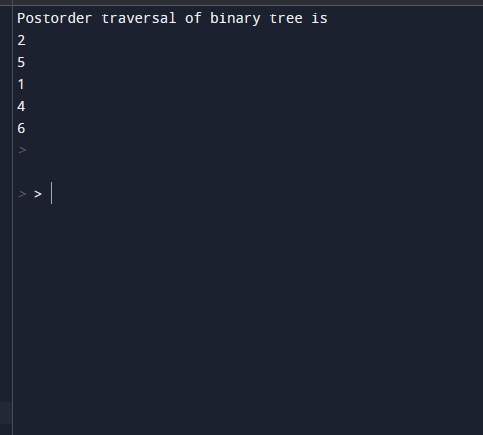
print("\nPostorder traversal of binary tree is")
postOrder(rootnode);
Output:
So here, according to the traversal algorithm, we shall design the tree manually and verify the output, which will make us understand the concept better.
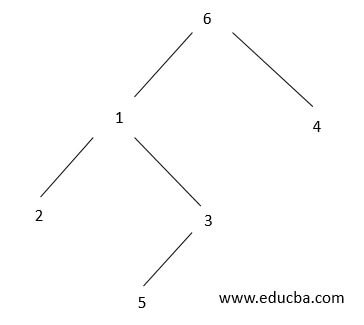
Based on the input, we have designed the binary tree above.
Explanation:
Root Node: 6
Left Node: 1
Right Node: 4
Left Node of Node 1: 2
Right Node of Node 1: 3
Left Node of Node 3: 5
Hence, the traversal will be as follows,
[2, 5, 3, 1, 4, 6]With this, we shall conclude the topic ‘Postorder Traversal’. We have seen what traversal is and its algorithm. Also implemented few sample examples to illustrate the traversal algorithm practically. A binary tree can be traversed in two types, Breadth-first traversal and Depth-first traversal. Depth-first traversal includes preorder, inorder, and traversals. Out of which, we have seen traversal here and will get to know of the other types in coming sessions. We have also listed out the Advantages and Disadvantages of traversal in the Binary tree.
Recommended Articles
This is a guide to Postorder traversal. Here we discuss How PostOrder traversal of the Binary tree works along with the advantages and disadvantages. You may also have a look at the following articles to learn more –

