Updated April 17, 2023

Introduction to Merge Sort in C
Merge sort is a sorting technique used for most of the problem solving related to sorting elements. Merge sort in C is related to the divide and conquer paradigm, which divides the input array into two arrays of different sizes which further calls the two divided array into two halves then those two arrays further then merges itself into next two and so on till all the elements get covered. The merge function is written in order to sort out the elements in proper format for simplified implementation as per requirement. Merge sort consists of a unique key for making all the comparisons related to sorting.
Syntax of Merge Sort in C
Merge sort in C does not have any particular syntax, but still, it follows some kind of steps and algorithm at the time of implementation, which is represented as follows:
The merge sort consists of some key for the comparison of elements within the arrays:
1. Let the two divided arrays be arr [k….o] and arr [o+1…y] and let the merge key include (arr, o, k, y).
2. The key include (arr, o, k, y) is the merge key which is used for comparison and merging into two halves.
3. Now, some of the scenarios are followed to make the comparisons, including the entire key and the parameters defined so far.
4. If key > 1, then that algorithm will work in a way where the middle point will be searched for, and then the array will get divided into two halves after comparison with the key using the below formula.
5. Call for the mergesort() function for the first half of the array from the bifurcated array.
Call merge_Sort (arr, k, o)
6. Call for the mergeSort() function for the next half of the array within the bifurcated array.
Call merge_Sort (arr, o, k, y)
How does Merge Sort work in C?
As mentioned before, that Merge sort is the sorting algorithm which works in the divide and conquer paradigm. So let’s see a bit about the divide and conquer technique. In the divide and conquer technique, it is needed to divide the problem into sub-problems in a recursive manner and then making it dig and divide into the next set or subset of problems, then making it final set by backtracking and combining the subset with the solution one layer above or below. There is one very important point to keep in mind regarding the divide and conquer algorithm is that the division and sub-structure following the division should not make the divided sub-problem change the actual problem defined and given at the starting point.
The main emphasizing and important steps to be followed are the three steps starting from divide conquer and then combining it so that it has to be from bottom to top fashion for the final result. Merge sort has some advantages associated with it regarding efficiency, and it is very important to get the merge sort in C in terms of time complexity. Merge sort will comprise one entire array, containing all the elements and its associated key, value pairs into it for comparison and manipulation with other sets of elements in the array. The associated subset available with the merge function has to be proper for further division and combination into final results. Merge sort is one of the algorithms which include playing around with the elements and indexing.
Merge sort further follows the following time complexity, thus making the entire algorithm efficient and fast as per requirement and implementation, which is as follows:
- If we try to estimate the worst-case time complexity, then it will be O (n*logn)
- If we try to estimate the best case time complexity, then It will be O (n*logn)
- If we try to estimate the Average time complexity, then it will be O (n*logn)
Then merge sort algorithm can be applied to sort the elements, and in an entire program, only the merge sort function can be used for any other working.
Example of Merge Sort in C
Given below is the example of Merge Sort in C:
This program demonstrates the implementation of a merge sort algorithm to sort the elements in their respective position in the order.
Code:
#include <stdio.h>
#define max_vl 12
int x_0[12] = { 11, 18, 16, 17, 27, 20, 33, 34, 31, 25, 0 };
int y_0[8];
void merg_sort(int low_m, int mid_0, int uppr_0) {
int K_1, K_2, u;
for(K_1 = low_m, K_2 = mid_0 + 1, u = low_m; K_1 <= mid_0 && K_2 <= uppr_0; u++) {
if(x_0[K_1] <= x_0[K_2])
y_0[u] = x_0[K_1++];
else
y_0[u] = x_0[K_2++];
}
while(K_1 <= mid_0)
y_0[u++] = x_0[K_1++];
while(K_2 <= uppr_0)
y_0[u++] = x_0[K_2++];
for(u = low_m; u <= uppr_0; u++)
x_0[u] = y_0[u];
}
void sort_0(int low_m, int uppr_0) {
int mid_0;
if(low_m < uppr_0) {
mid_0 = (low_m + uppr_0) / 2;
sort_0(low_m, mid_0);
sort_0(mid_0+1, uppr_0 );
merg_sort(low_m, mid_0, uppr_0);
}
else {
return;
}
}
int main() {
int u;
printf("Before_Sorting\n");
for(u = 0; u <= max_vl; u++)
printf("%d ", x_0[u]);
sort_0(0, max_vl);
printf("\nAfter_Sorting\n");
for(u = 0; u <= max_vl; u++)
printf("%d ", x_0[u]);
}Output:
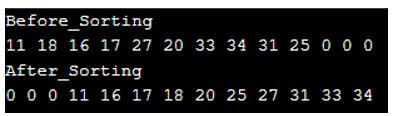
Explanation:
- If we go through the code, it has first considered the set of elements in an array, and then manipulation is performed for following the divide and conquer paradigm using the merge function.
- Then sorting algorithm is applied, followed by the merge function, thus providing the required output as shown in the output above.
- The set of elements given in an array or sorted after applying the merge sort in C.
Conclusion
Merge sort is quite a useful algorithm in terms of efficiency as it follows the divide and conquers paradigm. This divide and conquer way is efficient because it helps in making the entire problem into sub-problems, making the computation and sorting process easy while keeping the original problem the same. Furthermore, it helps programmers to adopt this sorting because of its easy and simplified nature in terms of understanding.
Recommended Articles
This is a guide to Merge Sort in C. Here we discuss the introduction, how merge sort works in C? and example, respectively. You may also have a look at the following articles to learn more –


