Updated March 18, 2023

Introduction to Matrix Multiplication in Java
Matrices in Java are stored in arrays. There are one-dimensional arrays and two-dimensional arrays that are present, which stores values in the form of matrices in the dimensions known as arrays. There are only numbers stored in one dimension in one dimensional array, while in two-dimensional arrays, numbers are stored in the form of rows and columns. Matrices can be used to add, subtract and multiply numbers in the Java programming language. Matrix multiplication is one of the most complicated tasks in Java programming methodology. We have to perform matrix multiplication in Java in this article and show how we can multiply two matrices and provide a reasonable output.
General Methodology
The matrix multiplication in the Java programming language is carried out in a very simple fashion. First, we input the numbers in the first two-dimensional array and then we enter the numbers of the elements in the second two-dimensional array. The numbers are added row-wise, which means that the first row is created, then the numbers in the second row are created and so on. Then the second matrix is created in a similar fashion, and then we start multiplying the numbers in the matrices.
Examples of Matrix Multiplication in Java
Below are the examples of matrix multiplication
Example #1
In the coding example, we see how two matrices are entered row-wise and then the matrix multiplication is carried out. The code for the multiplication of two matrices is shown below. There are three arrays that are declared. The product of the first and second matrices are shown inside the third matrix. Then the matrix is shown as an output which is a product of two matrices in the array.
Code:
import java.util.Scanner;
public class MatixMultiplication
{
public static void main(String args[])
{
int n;
Scanner input = new Scanner(System.in);
System.out.println("Enter the number of rows and columns of the matrices. They must be equal.");
n = input.nextInt();
int[][] a = new int[n][n];
int[][] b = new int[n][n];
int[][] c = new int[n][n];
System.out.println("Enter the numbers of the first matrix. Numbers will be added row wise \n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
a[i][j] = input.nextInt();
}
}
System.out.println("Enter the numbers of the 2nd matrix. Numbers will be added row wise. \n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
b[i][j] = input.nextInt();
}
}
System.out.println("Generating the multiplication of matrices.....");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
for (int k = 0; k < n; k++)
{
c[i][j] = c[i][j] + a[i][k] * b[k][j];
}
}
}
System.out.println("The product of the matrices is shown as below");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
System.out.print(c[i][j] + " ");
}
System.out.println();
}
input.close();
}
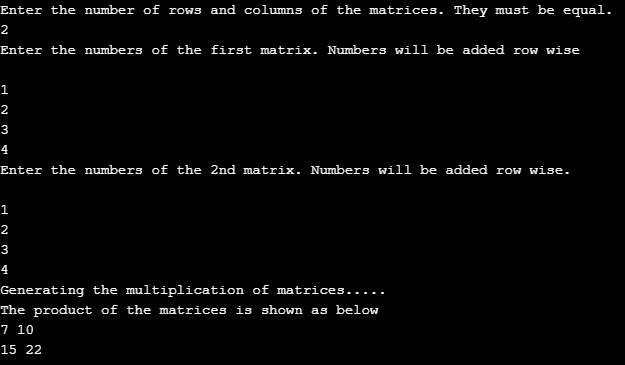
}The output for a 2*2 matrix is shown. The first matrix consists of elements as { 1,2
3,4}
and the second matrix also contains the same elements. In the sample output, we notice the multiplication of the matrices and the sample output. The elements of the matrix are produced in a very nice fashion. The output produced
{1,2 { 1,2 { 7, 10
3,4} * 3,4} = 15, 22}
Output:
Example #2
In coding example 2, we have the same program, but now we use 3-dimensional arrays for multiplication. We now use 3 * 3 matrix multiplication and show the output in another 3-dimensional array.
Code:
import java.util.Scanner;
public class Matix
{
public static void main(String args[])
{
int n;
Scanner input = new Scanner(System.in);
System.out.println("Enter the number of rows and columns of the matrices. They must be equal.");
n = input.nextInt();
int[][] a = new int[n][n];
int[][] b = new int[n][n];
int[][] c = new int[n][n];
System.out.println("Enter the numbers of the first matrix. Numbers will be added row wise \n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
a[i][j] = input.nextInt();
}
}
System.out.println("Enter the numbers of the 2nd matrix. Numbers will be added row wise. \n");
for (int z = 0; z < n; z++)
{
for (int k = 0; k < n; k++)
{
b[z][k] = input.nextInt();
}
}
System.out.println("Generating the multiplication of matrices.....");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
for (int k = 0; k < n; k++)
{
c[i][j] = c[i][j] + a[i][k] * b[k][j];
}
}
}
System.out.println("The product of the matrices is shown as below");
for (int k = 0; k < n; k++)
{
for (int l = 0; l < n; l++)
{
System.out.print(c[k][l] + " ");
}
System.out.println();
}
input.close();
}
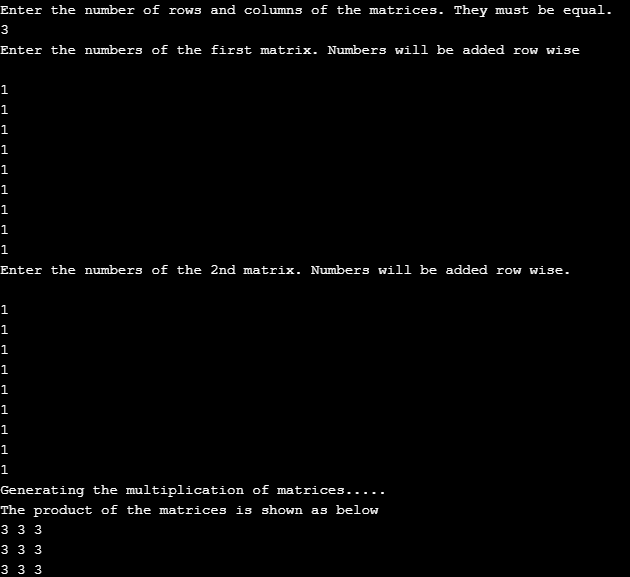
}From the second sample code, we print two 3 * 3 matrices. The first matrix is {1,1,1
1,1,1
1,1,1}
and the second matrix is also the same. The matrix multiplication is generated in the following ways
{1,1,1 {1,1,1 { 3,3,3
1,1,1 * 1,1,1 = 3,3,3
1,1,1} 1,1,1} 3,3,3}
Output:
Conclusion
In this article, we see the multiplication of a 2 * 2 matrix and a 3 * 3 matrix and the output is shown in a very nice fashion. The outputs are clearly given. Using matrix multiplication, we can also create a 4*4 multiplication of a matrix. The base is asked in the first step of the program. We can create 5 * 5, 6 * 6 matrices as well. More the base more is the complexity of the program.
However, the simple multiplication of matrices is very useful in calculating the reflection of a point with the X-axis, Y-axis or the Z-axis as the axis of reflection. These simple concepts are used in coordinate geometry and are used in mathematical modeling of geometry applications.
Recommended Articles
This is a guide to Matrix Multiplication in Java. Here we discuss the introduction, general methodology with respective examples of Matrix Multiplication in Java. You can also go through our other suggested articles to learn more –


