Updated March 4, 2023

Introduction to Matlab Remainder
The following article provides an outline for Matlab Remainder. Remainder is obtained in division when 2 numbers can’t be divided exactly.
In division 4 quantities are involved.
- Dividend: The number which is to be divided.
- Divisor: The number ‘by which’ the ‘Dividend’ is to be divided.
- Quotient: The ‘multiplying factor’ by which ‘Divisor’ is multiplied to get it equal to or closest to the ‘Dividend’.
- Remainder: If the product Divisor * Quotient is not equal to the ‘Dividend’, then the lag is referred as ‘Remainder.
In Matlab we use ‘rem’ function for the purpose of finding the remainder of a division.
Syntax:
R = rem (A, B)
Description:
- R = rem (A, B) will return the remainder when ‘A’ is divided by ‘B’.
- A is dividend and B is Divisor.
- A range like A:B can also be passed as an argument. In this case, the entire range will be considered as ‘Dividends’ and we get an array of ‘Remainders’ respective to each dividend.
Examples of Matlab Remainder
Given below are the examples mentioned :
Example #1
In this example, we will take both dividend and divisor as integers.
For our first example, we will follow the following steps:
- Initialize the Dividend.
- Initialize the Divisor.
- Pass both Dividend and Divisor to the rem function.
Code:
A = 15
[Initializing the Dividend]B = 3
[Initializing the Divisor]R = rem(A, B)
[Passing Dividend and Divisor as arguments to the rem function] [Mathematically, if we divide A with B, we will get ‘0’ as remainder. This is because 3 exactly divides 15, leaving no remainder]Input:
A = 15
B = 3
R = rem(A, B)
Output:
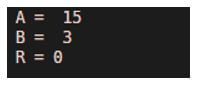
As we can see in the output, we have obtained the remainder of 15 and 3 as ‘0’.
Example #2
In this example, we will take a non-integer dividend and divisor as an integer.
For this example, we will follow the following steps:
- Initialize the Dividend.
- Initialize the Divisor.
- Pass both Dividend and Divisor to the rem function.
Code:
A = 6.7
[Initializing the Dividend]B = 3
[Initializing the Divisor]R = rem(A, B)
[Passing Dividend and Divisor as arguments to the rem function] [Mathematically, if we divide A with B, we will get ‘0.7’ as remainder. This is because 3 does not divide 6.7 exactly, and leaves 0.7 as remainder]Input:
A = 6.7
B = 3
R = rem(A, B)
Output:
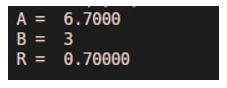
As we can see in the output, we have obtained the remainder of 6.7 and 3 as ‘0.7’.
Example #3
In this example, we will take both dividend and divisor as non-integers.
For this example, we will follow the following steps:
- Initialize the Dividend.
- Initialize the Divisor.
- Pass both Dividend and Divisor to the rem function.
Code:
A = 17.4
[Initializing the Dividend]B = 4.32
[Initializing the Divisor]R = rem(A, B)
[Passing Dividend and Divisor as arguments to the rem function] [Mathematically, if we divide A with B, we will get ‘0.12’ as remainder. This is because 4.32 does not divide 17.4 exactly and leaves 0.12 as remainder]Input:
A = 17.4
B = 4.32
R = rem(A, B)
Output:
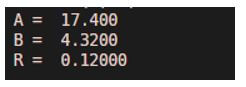
As we can see in the output, we have obtained the remainder of 17.4 and 4.32 as 0.12.
In the above 3 examples, we used rem function to get the remainder for single input.
Next, we will see how to use rem function for a range of dividends.
Passing a range of integers to the rem function will give an array output with remainder of each element when divided by the divisor.
Example #4
We will take a range of 5 to 10 and will use 4 as divisor.
For this example, we will follow the following steps:
- Initialize the range as [5:10]
- Initialize the Divisor
- Pass both Dividend range and Divisor to the rem function
Code:
A = [5 : 10] [Initializing the range of Dividends]
B = 4
[Initializing the Divisor]R = rem(A, B)
[Passing Dividend range and Divisor as arguments to the rem function] [Mathematically, if we divide every integer from 5 to 10 by 4, we will get the following remainders:1 2 3 0 1 2
Please note that these remainders correspond to division of elements of A by 4]
Input:
A = [5 : 10]
B = 4
R = rem(A, B)
Output:

As we can see in the output, we have obtained the array of remainders for the range passed as an argument.
Example #5
Let us take another example and take a range of 10 to 15.
For this example, we will follow the following steps:
- Initialize the range as [10:15].
- Initialize the Divisor as 3.
- Pass both Dividend range and Divisor to the rem function.
Code:
A = [10 : 15] [Initializing the range of Dividends]
B = 3
[Initializing the Divisor]R = rem(A, B)
[Passing Dividend range and Divisor as arguments to the rem function] [Mathematically, if we divide every integer from 10 to 15 by 3, we will get following remainders:1 2 0 1 2 0]
Input:
A = [10 : 15]
B = 3
R = rem(A, B)
Output:

As we can see in the output, we have obtained the array of remainders for the range passed as an argument.
Conclusion
‘rem’ function is used in Matlab to find the remainders during division. We can pass both single dividends or a range of dividends as argument to the ‘rem’ function.
Recommended Articles
This is a guide to Matlab Remainder. Here we discuss the introduction to Matlab Remainder along with examples for better understanding. You may also have a look at the following articles to learn more –

