Updated March 8, 2023

Introduction to Matlab Matrix Inverse
The following article provides an outline for Matlab Matrix Inverse. Inverse to any matrix, ‘M’ is defined as a matrix which, when multiplied with the matrix M, gives an identity matrix as output. The inverse matrix is represented by the notation M–1. So, as per the definition, if we multiply M with M–1 we will get an identity matrix in the output. The pre-requisite for a matrix to have an inverse is that it must be a square matrix, and the determinant of the matrix should not be equal to zero.
Syntax of getting Inverse of a Matrix in Matlab:
I = inv (M)
Description:
- I = inv (M) is used to get the inverse of input matrix M. Please keep in mind that ‘M’ here must be a square matrix.
Examples of Matlab Matrix Inverse
Given below are the examples of Matlab Matrix Inverse:
Example #1
In the first example, we will get the inverse of a 2 X 2 matrix.
Below are the steps that we will follow for this example:
- Define the matrix whose inverse we want to calculate.
- Pass this matrix as an input to the inverse function.
- Verify the result by multiplying the input matrix with the output matrix. This should give an identity matrix as an output.
Code:
M = [3 2 ; 2 1];
[Creating a 2 X 2 square matrix]I = inv(M)
[Passing the input matrix to the function inv] [Please note that, since we have used a 2 x 2 matrix as the input, our output matrix will also be a 2 X 2 matrix. This, when multiplied with the input matrix, will give an identity matrix as the output]I*M
[Code to verify that ‘I’ is inverse of ‘M’. This should give an identity matrix as the output]This is how our input and output will look like in the MATLAB command window:
Input:
M = [3 2 ; 2 1];
I = inv(M)
I*M
Output 1: (Inverse matrix)
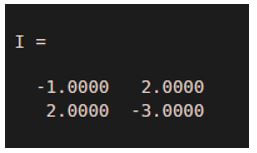
Output 2: (This should be an identity matrix)

As we can see in the output 1, the function ‘inv’ has given us the inverse of the input matrix. Output 2 verifies that ‘I’ is the inverse of ‘M’.
Example #2
In this example, we will get the inverse of a 3 X 3 matrix.
Below are the steps that we will follow for this example:
- Define the 3 X 3 matrix whose inverse we want to calculate.
- Pass this matrix as an input to the inverse function.
- Verify the result by multiplying the input matrix with the output matrix. This should give an identity matrix as an output.
Code:
M = [3 2 3; 4 2 1; 3 4 1];
[Creating a 3 X 3 square matrix]I = inv(M)
[Passing the 3 X 3 input matrix to the function inv] [Please note that, since we have used a 3 x 3 matrix as the input, our output matrix will also be a 3 X 3 matrix. This, when multiplied with the input matrix, will give an identity matrix as the output]I*M
[Code to verify that ‘I’ is inverse of ‘M’. This should give an identity matrix as the output]This is how our input and output will look like in the MATLAB command window:
Input:
M = [3 2 3; 4 2 1; 3 4 1];
I = inv(M)
I*M
Output 1: (Inverse matrix)
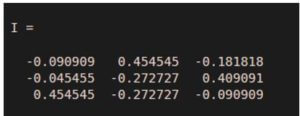
Output 2: (This should be an identity matrix)
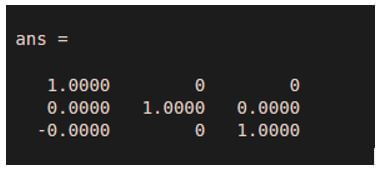
As we can see in the output 1, the function ‘inv’ has given us the inverse of the input matrix. Output 2 verifies that ‘I’ is the inverse of ‘M’.
Example #3
In this example, we will get the inverse of a 4 X 4 matrix.
Below are the steps that we will follow for this example:
- Define the 4 X 4 matrix whose inverse we want to calculate.
- Pass this matrix as an input to the inverse function.
- Verify the result by multiplying the input matrix with the output matrix. This should give an identity matrix as an output.
Code:
M = [1 3 3 6; 4 2 8 2; 3 3 4 5; 2 6 3 1];
[Creating a 4 X 4 square matrix]I = inv(M)
[Passing the 4 X 4 input matrix to the function inv] [Please note that, since we have used a 4 x 4 matrix as the input, our output matrix will also be a 4 X 4 matrix. This, when multiplied with the input matrix, will give an identity matrix as the output]I*M
[Code to verify that ‘I’ is inverse of ‘M’. This should give an identity matrix as the output]This is how our input and output will look like in the MATLAB command window:
Input:
M = [1 3 3 6; 4 2 8 2; 3 3 4 5; 2 6 3 1];
I = inv(M)
I*M
Output 1: (Inverse matrix)

Output 2: (This should be an identity matrix)
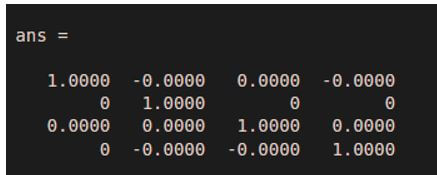
As we can see in the output 1, the function ‘inv’ has given us the inverse of the input matrix. Output 2 verifies that ‘I’ is the inverse of ‘M’.
Conclusion
Inverse to any matrix, ‘M’ is defined as a matrix which, when multiplied with the matrix M, gives an identity matrix as output. We use function ‘inv’ in Matlab to obtain the inverse of a matrix. We can only find the inverse of a square matrix.
Recommended Articles
This is a guide to Matlab Matrix Inverse. Here we discuss the introduction to Matlab Matrix Inverse along with examples respectively. You may also have a look at the following articles to learn more –

