Updated March 23, 2023
Introduction to Matlab Inverse Function
In Matlab, the Inverse function is obtained by applying the ‘ finverse ’ command. This command returns the value of the given function variable. In finverse f stands for function and after finverse, there will be parameters or argument list inside the brackets depending upon the requirement. if function depends only on one variable then inside bracket there will be one argument which if function (f) and if function depends on two arguments then there will be two parameters inside the brackets.
Syntax:
There are two syntaxes, it varies depending upon variable dependency.
Y = finverse (f)
This command is used if there are multiple variables in the function.
Y = finverse (f, var)
this command is used if there is only one dependent variable in function.
Examples of Matlab Inverse Function
The examples of Matlab Inverse functions are given below:
1. The inverse of cos x
sym x ;
Y ( x ) =
Cos ( x )
z = finverse ( y )
Z ( x ) =
a cos ( x )
| Input program | Command window | Comments |
| >> sym x ; | Input x | |
| >> y ( x ) = cos ( x ) | y(x) = cos ( x ) |
Inverse of ‘ y ’ with respect to independent variable ‘ x’ |
| >> z = finverse ( y ) | Z ( x ) = a cos( x ) |
The output of inverse of ‘ y ’ |
2. Inverse of 1/tan(x)
sym x ;
y ( x ) = 1 / tan ( x )
Y ( x ) =
1 / tan ( x )
z = finverse ( y )
Z ( x ) =
a tan ( 1 / x )</code
| Input program | Command window | Comments |
| >> sym x ; | Input ‘ x ’ | |
| >> y ( x ) = 1 / tan ( x ) | Y ( x ) = 1 / tan ( x ) |
The inverse of ‘ y ’ with respect to independent variable ‘ x ’ |
| >> z = finverse ( y ) | Z ( x ) = a tan ( 1 / x ) |
The output of inverse of ‘ y ’ |
3. The inverse of exponential ( x – 5 y )
syms x y
finverse ( exp ( x - 5 * y) , x )
ans =
5 * y + log ( x )
| Input code | Command window | Comments |
| Syms x y | Input parameters ‘ x ‘and ‘ y ’ | |
| Finverse ( exp ( x – 5 * y ) , x ) | ans =
5*y+log(x) |
The output of a function with respect to two variables |
4. The inverse of log (x-y)
syms x y
finverse ( log ( x – y ), y )
ans =
x – exp ( y )
| Input code | Command window | Comments |
| Syms x y | Input parameters ‘ x ’ and ‘ y ’ | |
| finverse ( log ( x – y ), y ) | ans = x – exp ( y ) |
The output of a function with respect to two variables |
The Inverse of Matrix
To find the inverse of any matrix ‘inv’ command is used. Consider two variables u and v independently. Where v is output var and u is input variable. Then command to find inverse will be v = inv ( u ). Here u^-1 is almost equal to inv(u).
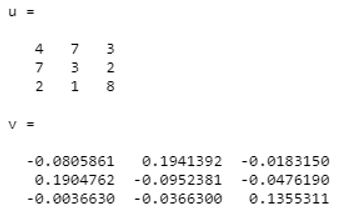
1. Matlab code to find the inverse of the above matrix;
Consider matrix u ;
| U = | 4 | 7 | 3 |
| 7 | 3 | 2 | |
| 2 | 1 | 8 |
u=[ 4 7 3; 7 3 2;2 1 8]
v=inv(u)
To obtain the inverse of the matrix there is one condition, the input matrix must be ‘square matrix’. otherwise, it will give the error. let see one example of the odd matrix (rectangular matrix).
2. Matlab code to obtain the inverse
Consider matrix U,
| U = | 6 | 6 | 8 |
| 4 | 4 | 6 | |
| 2 | 3 | 4 | |
| 9 | 1 | 2 |
u=[ 6 4 2 9; 6 4 3 1;8 6 4 2]
v=inv(u)
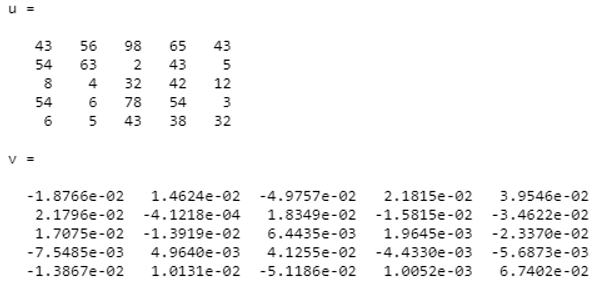
3. Matlab code to obtain inverse ;
Now consider,
| U = | 43 | 54 | 8 | 54 | 6 |
| 56 | 63 | 4 | 6 | 5 | |
| 98 | 2 | 32 | 78 | 43 | |
| 65 | 43 | 42 | 54 | 38 | |
| 43 | 5 | 12 | 3 | 32 |
u=[43 56 98 65 43;54 63 2 43 5;8 4 32 42 12;54 6 78 54 3;6 5 43 38 32]
v=inv(u)
Conclusion
Function inverse is one of the complex theories in mathematics but by using Matlab we can easily find out Inverse of any function by giving an argument list. One simple syntax is used to find out inverse which is ‘finverse’ followed by the variable specification.
Recommended Articles
This is a guide to Matlab Inverse Function. Here we discuss the inverse of the matrix along with the examples of Matlab Inverse Function. You can also go through our other suggested articles to learn more–