Updated April 18, 2023

Introduction to Linux List Directories
We know that the Linux system is made up of files and directories. At any stage, while working on the Linux command mode you may want to list all files and subdirectories in the directory. There are many ways to list the contents of the directories in our Linux system. In this article, we will discuss about what are the command and options that are used to list directories in the Linux system.
Commands Used to List Directories
There are many commands used to list files and directories in the Linux system. Let us discuss them one by one.
1. ls Command
The ls command is the basic command used to list files and directories within the Linux file system. But if you want to list only directories, ls command offers some options. Let us discuss them with examples.
How to List Directories Using Wildcards
The simplest method to list directories is using wildcards.
ls –d */Output:
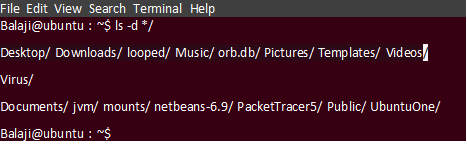
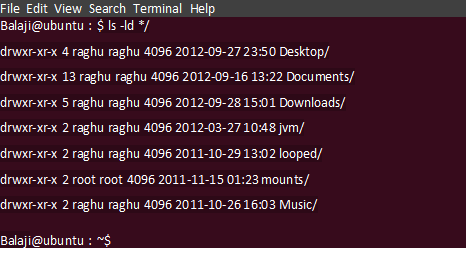
To list directories in the Long listing format use the -l option.
ls -ld */Output:
Using grep and -f option
The -F option adds a trailing forward slash. This option allows us to grep directories by ‘grep’ing lines that ends with forward slash.
ls -lF | grep \/$using grep and -l option
While using the long listing option –l we can grep the lines that starts with d. we can print only the directory names by using the following command.
ls -l | grep ^d | awk '{print $8,$9}'2. Using dir Command
The dir command is used to list the contents of the directory. The syntax is as follows.
dir -FOutput:
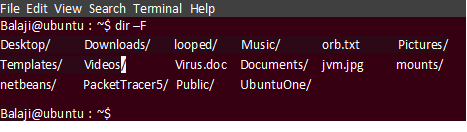
The forward slash in the above output indicates the directory and others indicate files. To print the detailed information of each file and directory use the -l command-line option.
dir -lOutput:
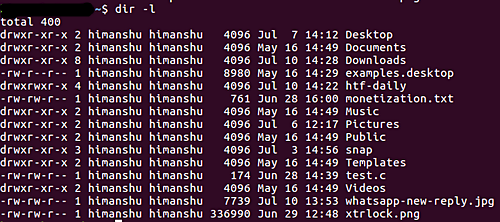
In the above output, d indicates directories.
3. Using printf Command
This command is used for formatting and printing text. It will display the given parameters in the specified format or execute the command depending on the option specified. To display the contents of current working directory run the following command.
printf '%s\n' *The output will display both files and directories.
4. Using find Command
The find command helps us to look up for files for which we know only the approximate names.In simple words the find command searches for a file in the current working directory and recursively through the subdirectories that matches the given search criteria. You can search files by name, extension, group, modification date, permissions etc.
To display all files which are present in the current working directory, use the following command.
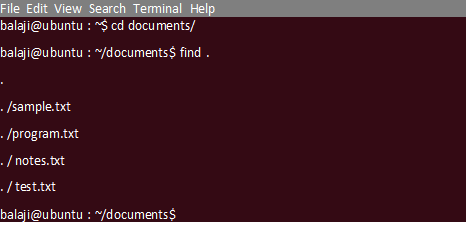
find.The dot (.) symbol indicates the current working directory.
cd documents/
~/documents$ find .Output:
How to List only Directories Using Find Command
If you want to search only the directories and skip the file names use the -type d option as shown below.
find / -type d -name "apk" -ls5. Listing Directories Using Stat Command
This command is used to display the information of files and filesystem. With the help of this command, we can find the properties of file such as file size, permissions, modified date, etc.
Use the following command line to list the files and directories
stat -c '%A %n' *6. Listing Directories Using Grep Command
This command is used for searching text files using regular expressions. To list the contents of the directory using grep command run the following command.
grep -l '.*' ./*7. Listing Directories Using Lsattr Command
To list the files and directories in the current directory use the following command.
lsattr ./*This command displays only the contents of the directory just down one level which means it cannot display other subdirectories and its contents and also hidden files.
8. Listing Directories Using Getfacl Command
The getfacl and setfacl are two of the mostt important and useful commands every system administrator should know to set the Access Control Lists of the files and directories.
To display the files and directories in the current working directory, just run the following command.
getfacl ./*The key features of this command is that it not only lists the contents of the directory but also other details such as
- Owner of the file or directory
- All the group names which has access to the file or directory
- Access rights to group, owner and others.
9. Listing Directories Using for Loop
This is another method to list the contents of the directory. Use the following command shown below.
for i in *; do echo $i; done10. Listing Directories Using Vim Editor
In addition to viewing and editing files, vim editor can also be used for listing files and directories. We already know that everything is considered as a file in Linux. This implies that a directory is also a file which contains some list of files and subdirectories.
To list the files and directories in the current working directory using vim editor, run the command shown below.
vim.The dot (.) at the end of the command implies the current working directory. Inorder to list the information of a specific directory, run the following command.
vim<path-to-dir>For Example:
vim documents/We can use the up and down keys to navigate through the screen. To list the contents of the subdirectory, place the cursor on the subdirectory and then press ENTER key.
11. Listing Directories Using Tree Command
This command is used to list the directory contents in a tree like format.
treeThe above command will list the files and subdirectories of the current directory. To list the directory contents down one level, run the following command.
tree -L lRecommended Articles
We hope that this EDUCBA information on “Linux List Directories” was beneficial to you. You can view EDUCBA’s recommended articles for more information.


