
Introduction to Laplace Transform MATLAB
MATLAB is a programming environment that is interactive and is used in scientific computing. It is extensively used in many technical fields where problem-solving, data analysis, algorithm development, and experimentation are required. The discipline-specific software is extensively written using MATLAB.
This article will study the MATLAB function used to calculate the Laplace transform. Before we get into details of how the Laplace function works in MATLAB, let us refresh our understanding of the Laplace transform.
Laplace transformation is used to solve differential equations. In Laplace transformation, the time domain differential equation is first converted into an algebraic equation in the frequency domain. Next, we solve this algebraic equation and transform the result into the time domain. This will be our solution to the differential equation. In simpler words, Laplace transformation is a quick method to solve differential equations.
Syntax
Let us understand the syntax of the Laplace function in MATLAB
Laplace (f)
Description of Laplace function in MATLAB:
- laplace (f) returns the Laplace transform of the input ‘f’.
Examples to Implement Laplace Transform MATLAB
Let us now understand Laplace function with the help of a few examples
Example #1
In the first example, we will compute laplace transform of a sine function using laplace (f): Let us take asine signal defined as:
- 4 * sin (5 * t)
Mathematically, the output of this signal using laplace transform will be:
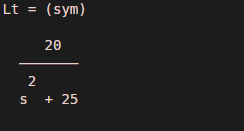
- 20/ (s^2 + 25), considering that transform is taken with ‘s’ as the transformation variable and ‘t’ as the independent variable.
Syntax
syms t[Initializing the variable]
f = 4*sin(5*t);[Input sine function]
Lt = laplace(f)[Using the laplace function to get the laplace transform]
Code:
syms t
f = 4*sin (5*t);
Lt = laplace (f)
Output:
As we can see, the transform is in terms of the variable ‘s,’ and the output is as expected by us.
Example #2
Here is an example where we compute laplace transform of a cosine signal using laplace (f):
Lets us take cosine signal defined as:
- cos (t) + cos (3 *t) ;
Mathematically, our output should be:
- s / (s ^ 2 + 1) + s / (s ^ 2 + 9)
Syntax
syms t[Initializing the variable]
f = cos (t) + cos (3 *t) ;[Input cos function]
Lt = laplace(f)[Using the laplace function to get the laplace transform]
Code:
syms t
f = cos (t) + cos (3 * t) ;
Lt = laplace (f)
Output:
As we can see, the Laplace transform is calculated w.r.t ‘s,’ and the output is as expected by us.
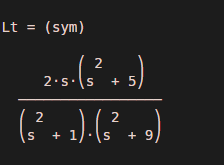
Example #3
In the next example, we will compute Laplace transform of an exponential function using laplace (f):
Lets us take an exponential function defined as:
- exp (-2*a^2);
Mathematically, our output should be:
- (2^ (1/2) *pi^ (1/2) *exp (s^2/8) *erfc( (2^ (1/2) *s) /4) ) /4
Syntax
syms a[Initializing the variable]
f = exp (-2 *a^2) ;[Input exponential function]
Lt = laplace(f)[Using the laplace function to get the laplace transform]
Code:
syms a
f = exp (-2 *a^2);
Lt = laplace (f)
Output:
As we can see, the laplace transform is calculated w.r.t ‘s’, and the output is as expected by us.
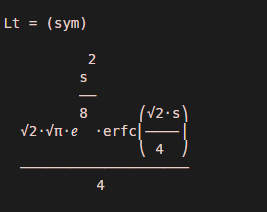
Example #4
Next, we will learn to calculate Laplace transform of a matrix. In the case of a matrix, the function will calculate laplace transform of individual elements of the matrix.
Below is the example where we calculate the Laplace transform of a 2 X 2 matrix using laplace (f): Let us define our matrix as:
- Z = [exp (2x) 1; sin (y) cos (z) ];
Now for each element in the matrix, we must pass transformation & independent variables.
- Let us define our independent variables as:Variables = [w a; b c];
- And Transform variables as:Transfrom_Variables = [p q; r s];
Mathematically, our output should be:
- [ exp (2x) /p, 1/q] [ sin (y) /r, cos (z) /s]
Syntax
syms a b c w p q r s[Initializing the variables]
Z = [exp (2x) 1; sin (y) cos (z)];[Input matrix with different signals]
Variables = [w a; b c];[Independent variables]
Transfrom_Variables = [p q; r s];[Transformation variables]
laplace(Z,Variables,Transfrom_Variables)
Code:
syms a b c d w x y z
Z = [exp (2*x) 1; sin (y) cos (z)];
Variables = [w a; b c];
Transfrom_Variables = [p q; r s];
laplace (Z, Variables, Transfrom_Variables)
Output:
As we can see, we have got the laplace transform of every element in the matrix Z.
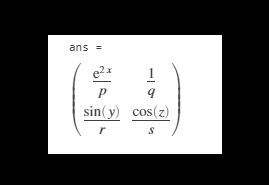
Conclusion
In MATLAB, you can use the Laplace function to calculate the Laplace transform of a function. We can calculate the Laplace transform w.r.t to the default transformation variable‘s’or the variable we define as the transformation variable.
Recommended Articles
This is a guide to Laplace Transform MATLAB. Here we discuss an introduction to Laplace Transform MATLAB, syntax, and examples for better understanding. You can also go through our other related articles to learn more –

