Introduction to Else if in R
A conditional statement that is used to validate a certain condition after the condition is proved false in the IF statement and subsequently gets passed to it in the sequence of conditional statements, returning a False by it to passes the control either to the next else if in the conditional block, or to else if no more else if is thereafter it, and executes successfully all the statements under it if the condition is proved true, with statement resembling else if statement structure of several other programming languages, is referred to as else if in R programming.
Syntax:
- Else if in R language is reserved keywords and it resides inside the if-else block and processes the associated expression based upon the conditions.
- Following is the else if syntax in R language:
if (condition){
# expression
} else if (condition){
# expression
} else if (condition){
# expression
} else {
# statement
}
- Condition is written inside () and the expression is written inside { }, the number and position of opening and closing parenthesis determines the scope of the else if and if statements.
- The number of else if block depends upon the programming logic or subroutine implementations.
- Also, the number of expressions or logic inside an else if block may vary depending upon business logic requirements.
- The else if block supports nested or multiple sets of if statement followed by else if statement inside its scope based upon the programming logic.
- In some cases else block is an optional part.
- It is a programming best practice to put default expressions in the else block which increases the program efficiency and code completeness.
Flowchart
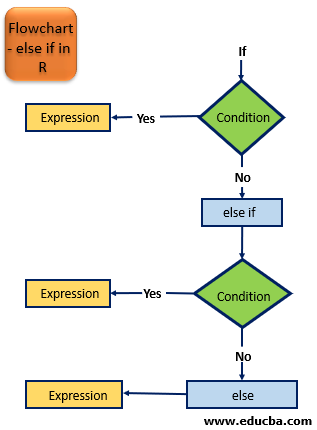
- The flow chart shown in the below image contains one else if block which is associated with if statement block and else statement block.
- The ‘else if’ and else keyword is represented in green color in the flowchart diagram.
- The condition is represented in blue color which evaluated as the TRUE or FALSE and routes to Yes or No direction.
- The expression is replanted as gray color which indicates the processor including single or a group of statements.
How Else if Statement Works in R?
1. The if-else and else if keywords allow associated with conditions for evaluation.
2. The condition return TRUE or FALSE value based upon the condition statement.
3. When the R program starts checking line by line in the code in the run time:
- It first checks and evaluates the return value of the condition present with the If statement.
- If the condition returns a TRUE Boolean value, R routed inside the if block and process for the expression or programming logic written in that block.
- If it founds the FALSE Boolean value, it will not go inside the If block, rather it will check for next available else if block.
- And program control moves to the else if statement if it found in the sequence of if-else if syntax.
- In the next step, it will check and evaluate the condition statement associated with the else if block.
- If the condition statements associated with else if block evaluated to return a TRUE boolean value, R process the code available inside the else if block.
- However, if the condition of else it returns a FALSE boolean value, R ignores the code and checks for next else if statement.
- If it founds another else if block subsequently, it processes the else if block in the same way.
- This iteration goes on until all the available else if block found for the if block scope.
- In the event of R runtime not found any else if block, it will search for else statement and process the code associated with the else block. And completes the IF else checking logic.
- And in the event, if R runtime not found any else if or else block it completes if-else checking logic immediately after the if block scope.
Examples of Else if in R
Given below are examples using R studio IDE with R terminal.
Business Scenario
There are four inventory bins present in a manufacturing company, Items are stored in multiple bins based upon the Item Number identification, R program will assign the Bin Items to vectors and implement else if logic to find a particular item Bin and display the respective bin information. This R code will represent the inventory bin tracking for an Item.
We will declare assign values 4 vectors in R code as follows:
R Code:
# Assign vector values
Inventory_bin_A <- c("Item1","Item2","Item8","Item42")
Inventory_bin_B <- c("Item28","Item74","Item86","Item6","Item48")
Inventory_bin_C <- c("Item258","Item64","Item96","Item62","Item18")
Inventory_bin_D <- c("Item23","Item86","Item31","Item66","Item90")
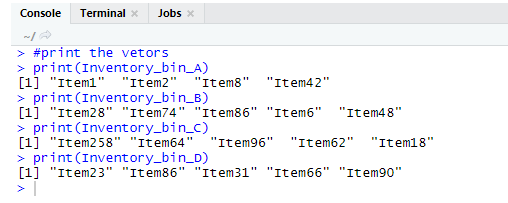
- We will print the vectors in R studio to check the assignment happened correctly on the console.
R code:
#print the vectors
print(Inventory_bin_A)
print(Inventory_bin_B)
print(Inventory_bin_C)
print(Inventory_bin_D)
Output:
- In the next step, we will implement else if statement in R to check ‘Item86’ belongs to which inventory bin.
R Code:
# writing else if logic to search Item86 #
if("Item86" %in% Inventory_bin_A){
print('Item86 found on Inventory_bin_A')
} else if("Item86" %in% Inventory_bin_B){
print('Item86 found on Inventory_bin_B')
} else if("Item86" %in% Inventory_bin_C){
print('Item86 found on Inventory_bin_C')
} else if("Item86" %in% Inventory_bin_D) {
print('Item86 found on Inventory_bin_D')
} else{
print('Item86 not available in the inventory bins')
}
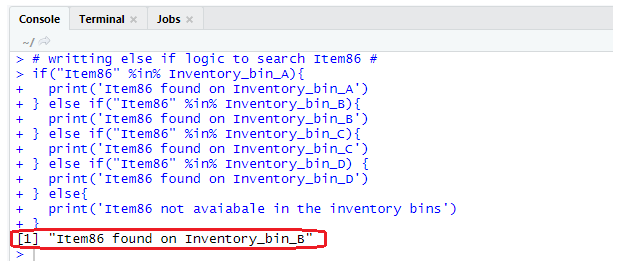
Output:
- The R console output shows Item86 found on Inventory_bin_B.
- As you observed in the assignment output Inventory, Item86 preset in two bins:
- Inventory_bin_B
- Inventory_bin_D
- Based upon the example R check the TRUE Boolean return value from the condition, Once it gets 1st occurrence of the TRUE condition, it does not check for further else if condition.
- Next, we will remove Item86 from bin Inventory_bin_B and run the code again.
R Code:
# Removing Item86 from Bin B
Inventory_bin_B<-Inventory_bin_B[!Inventory_bin_B %in% c("Item86")]
print(Inventory_bin_B)
Output:
- Now the Item86 is not available in Inventory_bin_B
- We will run the else if code again and check the output
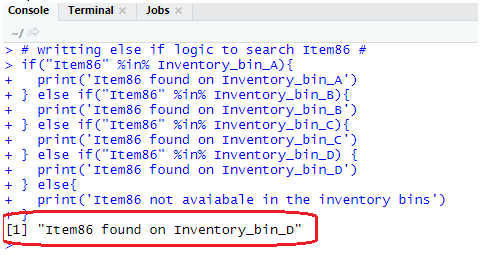
Output:
This R console output shows the updated Inventory ‘Inventory_bin_D’ bin information through the else if code.
Conclusion
Else if in R language is one of the handy programming features that can be implemented in several places like inside a loop or outside a loop condition. It helps the R programmers to write simplified logic and provides better code blocks development. The else if block increase code readability.
Recommended Articles
This has been a guide to Else if in R. Here we discuss the syntax, how Else if Statement Works in R?and examples. You may also have a look at the following articles to learn more –