Updated April 18, 2023

Definition of Binary Search Tree Python
Binary Search Tree in Python is an ordered or sorted tree whose internal nodes are in a way where they are attached to each other and can communicate with each other seamlessly. The concept of a binary search tree comes with a fact that nodes are arranged and organized in a way where addition, fast lookup, and removal of data items is used for manipulation followed by the creation of lookup tables and dynamic sets. Key and value pair play an important role for subtree to be in node’s left or right.
Syntax:
The syntax flow for the binary search Tree in Python is as follows:
class A_node:
def _init_(self, key),
#Put and initialize the key and value pait
#Then a utility function as per requirement can be written
def insert(root, key)
#define function
#Write the driver program & print with a logger to understand the flow.How Binary Search tree works in Python?
Binary Search Tree works in the following way let’s take this example to get illustrated. Let’s assume that below is the binary tree and it is in a way where there is no ordering or sequence maintained then how will a tree with so many varied numbers compare and arrange itself.
Basically, a binary tree is a node-based binary tree data structure that has the following characteristic
- The left subtree of a node contains nodes with keys lesser than the node’s key.
- Then, the right subtree of a node contains a key greater than the node’s key.
- The left and right subtree must have a binary search tree where the duplicate nodes are not all allowed.
- All the above three nodes must have keys for operations like insertion, deletion search of minimum and maximum.
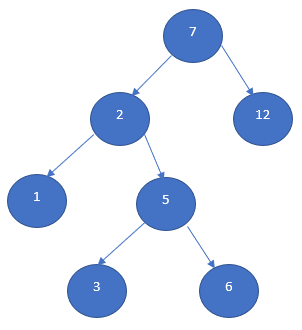
Since a Binary tree is considered a data structure it helps in storing data or numbers in an organized manner.
- The order present is proportional to half of the remaining values that makes it entirely less for computation or manipulation when it comes to maintaining the time complexities religiously.
- This is far better than linear time which is basically used for storing data i.e., the items stored in the form of key and value which makes it quite slower than corresponding operations present on the hash table.
- Binary search tree is a rooted binary tree whose internal nodes mainly makes comparison study for storing the keys after making comparisons which distinguish a lot of sets, multisets, and items present in the tree.
- Basically, the comparisons are made, and a total preorder is maintained with a three-way comparison subroutine which is part of the actual routine.
- The time complexities associated with each of the traversals have some significance in the sense it depends on how the elements are getting rotated left to right or vice versa like the worst case, best case, or average case.
- Duplicates are also allowed but then again restrictions are there with certain scenarios due to which sometimes they are not present or allowed.
Examples
Let us discuss examples of Binary Search Tree Python.
Example #1
This program demonstrates one of the utility functions of BST where a search is being made to make the key-value pair return some value with specific need and constraint.
def search_keyval (root_0, keyval):
if root_0 is None or root_0.keyval == key:
return root_0
if root_0.keyval < key:
return search (root_0.right,key)
return search_keyval (root_0.left,key)Explanation:
This is a custom search function written in python to make sure that the item needed in the entire BST is present for working as per requirement. This will help to make the subtree arranged with proper items in the entire tree.
Example #2
This program demonstrates the insertion of the key with value in the entire BST to perform manipulations and is shown in the output below.
class Node_def:
def __init__(self_0, key_1):
self_0.left = None
self_0.right = None
self_0.val = key_1
def insert_val(root_0, key_1):
if root_0 is None:
return Node_def(key_1)
else:
if root_0.val == key_1:
return root_0
elif root_0.val < key_1:
root_0.right = insert_val(root_0.right, key_1)
else:
root_0.left = insert_val(root_0.left, key_1)
return root_0
def inorder_val(root_0):
if root_0:
inorder_val(root_0.left)
print(root_0.val)
inorder_val(root_0.right)
r_9 = Node_def(50)
r_9 = insert_val(r_9, 12)
r_9 = insert_val(r_9, 20)
r_9 = insert_val(r_9, 2)
r_9 = insert_val(r_9, 15)
r_9 = insert_val(r_9, 60)
r_9 = insert_val(r_9, 76)
inorder_val(r_9)Output:
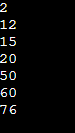
Explanation
In the given series of programs insertion of elements are made to arrange them in an order with some comparisons made as per requirement where the entire comparison and calculation is started from root till the end. There are some time complexities associated with this where search and insertion are made with comparison and search on heights and level wise where it is made with worst time complexity of O(h).
Example #3
This program demonstrates the binary search tree which represents the items present in the entire tree even with subtree containing elements in an ordered manner as shown in the output below.
class Node_0:
def __init__(self_3, data_0):
self_3.left = None
self_3.right = None
self_3.node = data_0
def insert(self_3, data_0):
if self_3.node:
if data_0 < self_3.node: if self_3.left is None: self_3.left = Node_0(data_0) else: self_3.left.insert(data_0) elif data_0 > self_3.node:
if self_3.right is None:
self_3.right = Node_0(data_0)
else:
self_3.right.insert(data_0)
else:
self_3.node = data_0
def Print_Tree(self_3):
if self_3.left:
self_3.left.Print_Tree()
print(self_3.node, end=' ')
if self_3.right:
self_3.right.Print_Tree()
root_0 = Node_0(18)
root_0.insert(5)
root_0.insert(24)
root_0.insert(2)
root_0.insert(22)
root_0.insert(18)
root_0.insert(11)
root_0.Print_Tree()Output:
![]()
Explanation: This program in binary tree tries to arrange all the elements within it in a hierarchy for making elements arranged in order for representing each element that has some value in it. Node_0 then performs and calculates the time complexity of the entire binary search tree.
Conclusion
Binary_Search_Tree in Python is used for a lot of reasons and the significance behind selecting python is for its ease of use and seamless behavior that it provides. It even helps in making a lot of manipulations in left to right or right to left as per requirement. A binary search tree has lots of advantages in terms of making the iterative search in an ordered manner.
Recommended Articles
This is a guide to Binary Search Tree Python. Here we discuss the introduction, syntax, and working of the Binary Search tree in Python along with different examples and code implementation. You may also have a look at the following articles to learn more –


