Updated March 15, 2023
Introduction to TensorFlow Regression
Linear regression tensorflow is the model that helps us predict and is used to fit up the scenario where one parameter is directly dependent on the other parameter. Here, we have one dependent variable and the other one independent. Depending on the change in the value of the independent parameter, we need to predict the independent change variable.
There are various ways in which we can fit the model by using the linear regression methods. In this article, we will have a general look at What is tensorflow regression, using tensorflow regression, creating the model, and understanding its implementation and the help of an example. Finally, we will conclude our statement.
What is TensorFlow Regression?
Linear regression is the model of the tensorflow that works along with the independent and errors that are distributed identically. These errors are generated considering the autocorrelation and the hetero scedasticity. The linear regression model comes with the support to users of the generalized feasible least squares and the AR (p) that are nothing but auto-correlated errors, generalized Least Squares, Weighted Least Squares, and Ordinary Least Squares. The commands and the parameters of each one differ concerning their usage.
The simple example of linear regression can be represented by using the following equation that also forms the equation of the line on a graph –
B = p + q * A
Where B and A are the variables, B is the dependent variable whose value changes concerning A’s value. A is the independent variable and the input value we pass to our regression model. B is also called the value or output whose value is to be predicted or estimated. The q is the slope of the regression line, representing the effect that A has over the value of B. p is the constant value that also represents the y-intercept, the point where the regression line touches the Y-axis.
There are two types of regression –
- Simple linear regression
When only one independent variable is there that’s varying in value; we want to predict the value of one dependent variable that depends on the independent variable. The implementation of this scenario’s situation is called Simple Linear Regression.
- Multiple linear regression
When multiple independent variables vary in their value, and we want to predict the value of one dependent variable that depends on all the independent variables, then the implementation of this situation is called Multiple Linear Regression.
Using TensorFlow Regression
We will need to create the model. Fit it into the regression pattern and then pass various regression functions. You can also print the output summary at the end if you want. Various parameters need to be passed.
The parameters involved in the description of implementing the linear regression are as specified below –
- Cholsimgainv – The n* n-dimensional triangular matrix array satisfies some constraints.
- Df_model – The float data type value represents the degree of freedom of the model, and the value is the same as p-1. Here, p stands for the regressors count. Whenever we calculate the degree of freedom here, we do not consider the intercept.
- Pinv_wexog is an array with the dimensions of p * n, which is more, and a Penrose pseudo-inverse matrix.
- Df_resid – It is a float value that corresponds to the degree of the freedom that s residual, and the value of the parameter is equal to n-p, where p is the count of passed parameters while n is the count of observations. Here the intercept is the parameter that counts the freedom degree.
- Nobs – this parameter represents the number of observations and is usually denoted by n.
- Llf is a float value representing the likelihood function corresponding to the fitted model.
- Sigma – It is an array having dimensions of n*n and represents a covariance matrix with an error term.
- Normalized cov params are an array of p* p dimensions with the normalized covariance values.
- Sigma – This is an array of n * n dimensions and a covariance matrix containing the error terms.
- Wendog – It is the whitened response variable and is of array data type.
- Wexog – It is an array and consists of the whitened design matrix.
How to use TensorFlow Linear Regression?
There are four available classes of the properties of the regression model that will help us to use the tensorflow linear regression. The classes are as listed below –
- OLS – Ordinary Least Square
- WLS – Weighted Least Square
- GLS – Generalized Least Square
- GLSAR – Feasible generalized Least Square and the autocorrelated errors.
We can use all the regression above models in the same way, following the same structure and methodologies. Other than rolling WLS, recursive LS, ad rolling OLS, the other regression classes have the superclass of GLS.
Create the model
To create a horsepower model, you can use the build_and_compile_model() function. For the tensor keras model, we can use the function tf.keras.Sequential()function.
TensorFlow Regression Examples
After you have learned the basics of using the tensorflow, it’s time to turn to a more sophisticated part where we will implement the linear regression in the source data with the help of the tensorflow package. We will follow the same steps mentioned in the above example with one additional part for the OLS model. Let us directly jump to code and then try to understand it –
// importing the necessary packages
import numpy as educbaSampleNumpy
import stateducbaSampleStatsodels.api as educbaSampleStats
// Loading the source data set
educba_data = educbaSampleStats.datasets.spector.load()
// Adding constants to the data file
educba_data.exog = educbaSampleStats.add_constant(educba_data.exog, prepend=False)
//Fitting the model which is in OLS
educbaModel = educbaSampleStats.OLS(educba_data.endog, educba_data.exog)
res = educbaModel.fit()
// Summarize the statistical results and printing the same on console
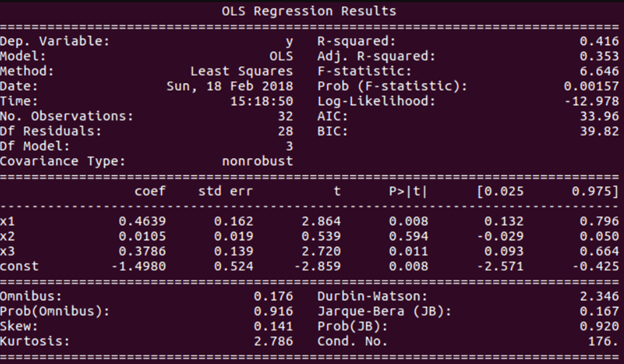
print(res.summary())
We can easily read the details of the result from the output. Execution of the above code gives the following output –
Conclusion
Tensorflow Linear regression model helps to predict or estimate the values of the dependent variables as and when there is a change in the independent quantities. Tensorflow Multiple regression is when you have multiple independent variables while one dependent variable is dependent on all the other independent ones.
Recommended Articles
This is a guide to tensorflow regression. Here we discuss the four available classes of the properties of the regression model that will help us to use the tensorflow linear regression. You may also have a look at the following articles to learn more –

