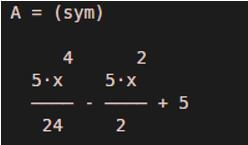Taylor Series Matlab

Updated March 13, 2023

Introduction to Taylor Series Matlab

The following article provides an outline for Taylor Series Matlab. Taylor series is used to expand a function into an infinite sum of terms. Taylor series expresses the function in terms of its derivative at a point.

Example:

Taylor series of e^x = 1 + x + x^2/2! + x^3/3! + x^4/4! + x^5/5! + …

As can see in the above example, we have drilled down the function ‘e^x’ into a polynomial which is of infinite degree. It finds its application in modern day Physics to simplify complex calculations, by breaking them down into the simple sum of terms. In Matlab, we use the ‘taylor’ function to get taylor series of any function.

Syntax:

A = taylor (Fx, p)

A = taylor (Fx, p, a)

A = taylor (Fx, Name, Value)

Explanation:

• taylor (Fx, p) will compute the Taylor series for the input function. By default, the series is computed till the 5^th order and at ‘p = 0’ as the point.
• taylor (Fx, p, a) will compute the Taylor series for input function at the point p = a.
• taylor (Fx, Name, Value) can be used to put additional conditions, which can be specified using pair arguments (Name, Value).

Examples of Taylor Series Matlab

Let us now see the code to calculate in Matlab using ‘taylor (Fx, p) function’:

Example #1

In this example, we will use a simple cos function and will expand it using Taylor series function.

We will follow the following 2 steps:

• Create the cos function in Matlab.
• Calculate the Taylor series using ‘Taylor function’.

Syntax:

syms x
[Initializing the variable ‘x’] A = taylor (5* cos (x))

[Creating the cos function and passing it as an input to the taylor function] [Please note that, since we did not pass any value for point ‘p’, the Taylor series will be computed at the point p = 0, by default] [Mathematically, the Taylor series of 5*cos(x) is (5*x^4)/24 – (5*x^2)/2 + 5]

Code:

syms x
A = taylor (5* cos (x))

Output:

Let us now see how the code for Taylor series looks like in Matlab if we want to use the point of our choice for Taylor series. For this purpose, we will be using ‘taylor (Fx, p, a)’ function and will pass some value for ‘p’.

Example #2

In this example, we will use a function of sine and will find the Taylor series at the point p = 1.

We will follow the following 2 steps:

• Create the function of sine in Matlab.
• Calculate the Taylor series using ‘taylor (Fx, p, a) function’ and pass ‘p’ as 1.

Syntax:

syms x
[Initializing the variable ‘x’] A = taylor(4*sin(x)) x, 1)

[Creating the polynomial function of sine and passing it as an input to the taylor function] [Please note that we have passed ‘x’, ‘1’ as arguments, which represent the point x = 1] [Mathematically, the Taylor series of 4*sin (x) at point x = 1 is4*sin(1) – 2*sin(1)*(x – 1)^2 + (sin(1)*(x – 1)^4)/6 + 4*cos(1)*(x – 1) – (2*cos(1)*(x – 1)^3)/3 + (cos(1)*(x – 1)^5)/30

Code: 

syms x
A = taylor(4*sin(x), x, 1)

Output:

Let us now see how the code for Taylor series looks like if we need to add more conditions using the ‘Name’, ‘Value’ pair arguments. For this purpose, we use ‘taylor (Fx, Name, Value)’ function.

Example #3

In this example, we will use the same polynomial function as used in the above example but will find the Taylor series only till 2^nd order.

We will follow the following 2 steps:

• Create the function of cos and sine.
• Calculate the Taylor series using the function ‘taylor (Fx, Name, Value)’.

Syntax:

syms x
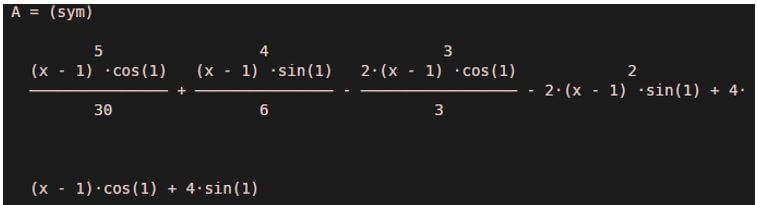
[Initializing the variable ‘x’] A = taylor ((5*cos (x) + 4*sin (x)), x, 1, 'Order', 2)

[Creating the polynomial function of cos & sine and passing it as an input to the taylor function] [Please note that we have passed ‘Order’, ‘2’ as name-value pair arguments] [Mathematically, the taylor series of 5*cos (x) + 4*sin (x) at point x = 1 and order 2 is 5*cos (1) + 4*sin (1) + (x – 1) * (4*cos (1) – 5*sin (1))]

Code:

syms x
A = taylor ((5*cos (x) + 4*sin (x)), x, 1, 'Order', 2)

Output:

Conclusion

A function’s Taylor series can be found in Matlab using taylor function. By default, the Taylor series is computed at point x = 0. If we need Taylor series w.r.t some other point, we can use taylor (Fx, p, a).

This is a guide to Taylor Series Matlab. Here we discuss the introduction to Taylor Series Matlab along with examples respectively. You may also have a look at the following articles to learn more –

1. Laplace Transform MATLAB
2. MATLAB Eigenvalues
3. Matlab plot title
4. Matlab Index Exceeds Matrix Dimensions