Updated November 21, 2023
What is the Taylor Rule?
The Taylor Rule, proposed by economist John B. Taylor in 1993, is like an indicator that tells central banks when they must raise their interest rates. It uses factors like inflation, output gap, etc., to determine the target short-term interest rates for monetary policies.
Taylor developed this formula from his analysis of the Federal Reserve’s monetary policy during 1987-1992, outlined in his study “Discretion versus policy rules in practice.” The rule helps the Federal Reserve to decide a target interest rate when the expected inflation rate and GDP growth differ from the target inflation and long-term GDP growth rate.
This rule suggests that when inflation is above the target rate, the central bank should raise interest rates in proportion to the extent by which inflation exceeds the target rate.
Table of Contents
- What Does it Mean?
- Principle Explained
- Formula
- How to Use it?
- Example
- Graph
- Limitations & Criticism
- Calculator
Key Highlights
- John B. Taylor proposed the Taylor rule in 1993 in his article “Discretion versus policy rules in practice.”
- It helps central banks to determine target short-term interest rates in response to inflation, output gap, and other economic indicators.
- Target Rate = Neutral Rate + 0.5 x (GDPe – GDPt) + 0.5 x (Ie – It).
- The rule has limitations and criticism, and policymakers must consider other factors when making policy decisions to remain flexible to changing economic conditions.
Taylor Rule Principles Explained
The principles of Taylor rule in economics are as follows.
| Rule # | Condition | Action | Result |
| #1 | If inflation is above the Fed’s inflation target. | Raise interest rates. | To mitigate inflation. |
| #2 | If the GDP/output gap is negative. | Lower interest rates. | To boost the economy. |
| #3 | If there is a deviation in inflation & output gap. | Adjust rates based on the weighted average. | To stabilize prices. |
Taylor Rule Formula
The following is the Taylor rule equation to calculate the target rate.
Where Neutral Rate = Real Policy Rate + Expected Inflation Rate
- Neutral Rate: It represents the existing short-term interest rate. You can calculate it by adding the real policy and expected inflation rates.
- GDPe: Expected GDP Growth Rate
- GDPt: Long-Term or Target GDP Growth Rate
- Ie: Expected Inflation Rate
- It: Target Inflation Rate
How Do You Use the Taylor Rule Formula?
The following is a step-by-step procedure to apply the Taylor rule formula
Step 1: First, determine the neutral rate, the short-term interest rate that the central banks want to continue under stable inflation and GDP growth conditions.
Step 2: Next, determine the expected GDP growth rate (GDPe).
Step 3: Find the long-term GDP growth rate (GDPt) observed over a specific period.
Step 4: Next, calculate the GDP growth rate deviation by subtracting the long-term rate from the expected rate (GDPe – GDPt).
Step 5: Next, identify the expected inflation rate (Ie).
Step 6: Next, determine the actual inflation rate (It) during the given period.
Step 7: Next, calculate the deviation in the inflation rate, which is the difference between the expected inflation rate and the target inflation rate, i.e., (Ie − It).
Step 8: Finally, apply the value in the following formula,
Target Rate = Neutral Rate + 0.5 x (GDPe – GDPt) + 0.5 x (Ie – It)
Example of Taylor Rule Formula (With Excel Template)
Let’s take an example to understand the calculation of the Taylor Rule Formula in a better manner.
Example #1
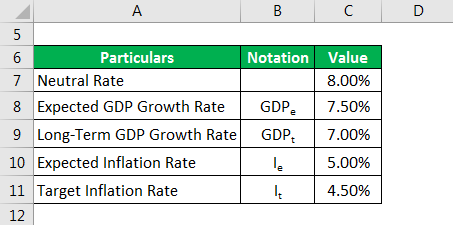
Consider a scenario where the country A’s long-term GDP growth rate stands at 7.0% while the target inflation rate is 4.5%. The current short-term interest rate in the economy is at 8.0%. However, the inflation rate is expected to increase to 5.0% and GDP growth to 7.5%. Let us calculate the new short-term interest rate based on the given information.
Given:
Solution:
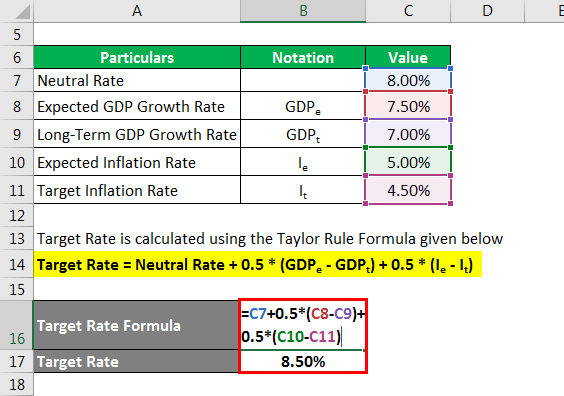
Let’s calculate the target rate using the following Taylor rule formula.
Target Rate = Neutral Rate + 0.5 x (GDPe – GDPt) + 0.5 x (Ie – It)
= 8.0% + 0.5 × (7.5% − 7.0%) + 0.5 × (5.0% − 4.5%) = 8.50%
Therefore, country A should increase the new short-term interest rate to 8.50%.
Example #2
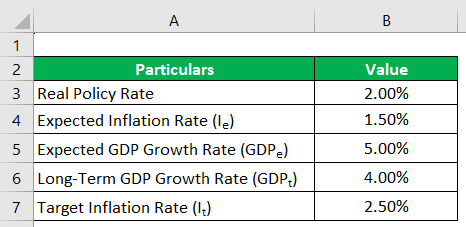
Suppose the real policy rate is 2% in Country B, and they expect prices to increase by 1.5%. Furthermore, the long-term GDP growth rate is 4.0%, and experts anticipate the GDP growth rate to reach 5.0% in the upcoming period. The target inflation rate set by policymakers is 2.5%. Let’s calculate the new target rate for country B.
Given:
Solution:
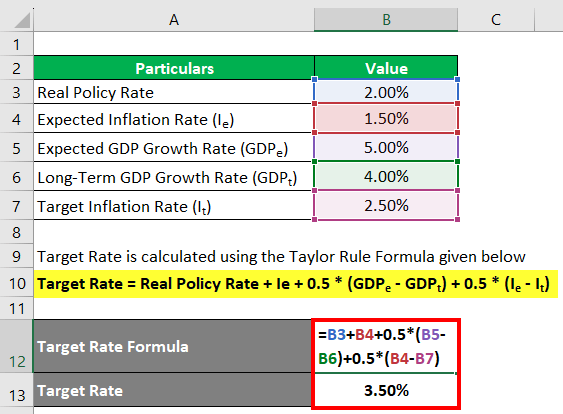
Now, let us calculate the target rate using the following formula.
Here, Neutral rate = Real Policy Rate + Expected Inflation Rate
So,
Target Rate = Real Policy Rate + Expected Inflation Rate + 0.5 x (GDPe – GDPt) + 0.5 x (Ie – It)
= 2.0% + 1.5% + 0.5 x (5.0% – 4.0%) + 0.5 x (1.5% – 2.5%) = 3.5%
Hence, the new target rate for Country B would be 3.5%. This short-term interest rate adjustment will help match the expected changes in GDP growth and inflation, maintaining economic stability.
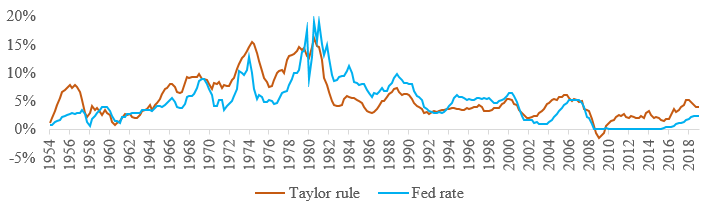
Taylor Rule Graph
The Taylor Rule is an essential guideline in economics and banking. It helps adjust short-term interest rates to stabilize the economy. For instance, if expected inflation is below the target or production is forecasted to be lower than potential, the Taylor Rule suggests using policies to boost economic growth. On the other hand, if the expected inflation rate or national production rises, it’s advisable to implement measures to slow down the economy.
Graph:
Key Curves on the Graph:
- Blue Line: It represents the interest rate the Federal Reserve sets.
- Orange Line: It shows the interest rate according to the Taylor rule.
Interpretation:
The graph shows the interest rates set by the FED and as calculated by the Taylor rule from 1954 to 2018. If we check the rates for 2018, the red line is higher than the blue line. As per the Taylor rule, the interest rates must be higher than they are. This way, the Taylor rule chart helps economists study the country’s current and required interest rates.
Limitations & Criticism
While the CFA Taylor rule is a popular guideline for central bank decision-making, it has some limitations and criticisms, which are as follows.
1. Relies on Inflation
The rule uses a GDP deflator to calculate inflation to evaluate the economy’s health. However, some economists argue that this approach is limited and ignores other indicators. Therefore, some policymakers recommend using the “Personal Consumption Expenditures” (PCE) deflator as an alternative.
2. Oversimplification
The rule is a simple equation and does not consider factors affecting the economy. It includes asset prices, exchange rates, unemployment rates, and other important economic variables. This may lead to incomplete or incorrect policy decisions.
3. Over-Reliance on Data
It requires accurate and timely data on inflation, economic growth, and other key variables. However, this data may be incomplete or revised, leading to errors in decision-making. Additionally, the rule prioritizes short-term data over long-term trends, potentially neglecting crucial insights.
4. Lack of Flexibility
It follows a fixed economic model, which may not be flexible enough to consider real-world economic conditions or development changes. Policymakers may completely rely on this model and fail to consider other factors that may be relevant.
5. Ignoring Fiscal Policy and Regulation
It does not consider the effects of fiscal policy and financial regulations, such as taxes or government spending changes. This omission can significantly impact the economy and cause conflicts with monetary policy goals.
Taylor Rule Calculator
You can use the following Taylor rule formula calculator:
| First Value | |
| Second Value | |
| Formula = | |
| = | First Value + 0.5 * (Second Value - Formula =) + 0.5 * ( - ) |
| = | 0 + 0.5 * (0 - 0) + 0.5 * (0 - 0) |
| = | 0 |
Final Thoughts
The Taylor rule guides central banks in adjusting interest rates based on inflation and the output gap. However, the rule has limitations, and critics argue that it may not be appropriate for all economic situations or during periods of excessive volatility. Nonetheless, it remains an influential framework for monetary policy, contributing to the development of more sophisticated policy rules and models over the years.
Frequently Asked Questions (FAQs)
Q1. What are the alternatives to the Taylor rule?
Answer: There are many alternatives that the Federal Reserve may use in place of the Taylor rule. The most common alternatives are as follows.
- Evans Rule: It adjusts interest rates by focusing on unemployment and inflation.
- Nominal GDP (NGDP) Targeting: It suggests a specific level of nominal GDP to make inflation and economic growth decisions.
- Price Level Targeting: It focuses on keeping a set price level and adjusts policies to achieve this goal.
Q2. What are the uses of the Taylor rule?
Answer: The following are some key uses of the Taylor rule.
- Central banks use it as a reference for adjusting interest rates.
- It helps to achieve macroeconomic goals like stable prices and maximum employment.
- It is useful to forecast future interest rates and make informed decisions based on economic conditions.
- It measures the effectiveness of monetary policy decisions in achieving objectives and determining their impact on the economy.
- It facilitates transparent communication between central banks, policymakers, and the public concerning decisions based on economic indicators.
Q3. Can the Taylor rule be negative?
Answer: Yes, if inflation is low or negative and the output gap is also negative, the original formula can result in a negative nominal interest rate. However, the rule doesn’t offer actionable guidance for policymakers in situations where interest rates could potentially turn negative. Moreover, it also faces limitations when interest rates hit zero (known as the zero lower bound).
Recommended Articles
We hope this EDUCBA article on the Taylor Rule was beneficial to you. For further guidance on economics-related topics, EDUCBA recommends these articles: