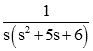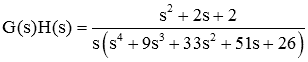Updated March 8, 2023
Introduction to Root Locus Matlab
The W.R. Evans developed the root locus method. It is widely used in control engineering for the design and analysis of control systems. In this method, system poles are plotted against the value of a system parameter, especially the open-loop transfer function gain root locus analysis is a graphical method for examining how the roots of a system change with variation of a certain system parameter are typically used in control theory and stability theory. In this topic, we are going to learn about Root Locus Matlab.
Syntax
The syntax for Root Locus Matlab is as shown below:-
rlocus (sys)
How to Do Root Locusmatlab?
In a Matlab for a root locus, rlocus inbuilt function is available. For using these inbuilt rlocus function, we need to create one transfer function on a Matlab; for that, we can use a tf inbuilt function which can be available on Matlab.
Let us see how we used these function to display the root locus. For that, first, we need to create one transfer function. For creating a transfer function, we need to know the coefficients of the numerator and denominator of that transfer function
we create transfer function in two ways. The ways are as follows:-
1. Num3= [25 ];
Den3 = [1 -1 -2];
TF1 = tf (Num3 , Den3)
In a first way, we can take two variables to store the numerator and denominator coefficients and then we just pass those two variables on tf function and that a comma separates two variables.
2. GH1 = tf([1],[1 5 6 0])
In the tf function, we take two square brackets; in the first square brackets, we write the coefficients of the numerator (order s^4, s^3……, s, constant), and in second square brackets, we write coefficients of the denominator (order s^4, s^3……, s, constant). The comma separates these two square brackets.
Then use rlocus function in brackets the variable which is assigned for the transfer function.
Examples of Root Locus Matlab
Here are the following examples mention below
Example 1
Let us consider one example,
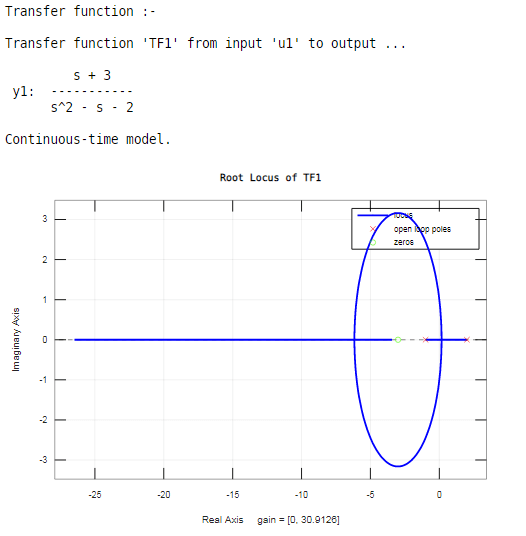
In this example, we take one transfer function for that we create two variables, ‘num1’ and ‘den1’, respectively. The variable ‘num1’ contains the coefficients of the numerator of the transfer function, and variable ‘den1’ stores the coefficients of the denominator of the transfer function. The tf function generates a transfer function for given coefficients of ‘num1’ and ‘den1’ variables on Matlab. Then using two variables of transfer function ‘num1’ and ‘den1’, we can display the transfer function and stored it in variable ‘TF1’.Then use the ‘rlocus’ function in brackets the variable which is assigned for transfer function ‘TF1’.
Code:
clc;
clear all;
close all;
num1= [1 3 ];
den1 = [1 -1 -2];
disp ('Transfer function :- ');
TF1 = tf (num1 , den1)
rlocus(TF1)
Output:
As shown in the resultant rot locus, it can show poles and zeros. For locating poles, the ‘×’ sign is used, and for zeros, the ‘o’ sign is used on a root locus.
Root locus exists on the real axis between:
2 and -1
-3 and negative infinity
Example 2
Let us see one more example related to root locus Matlab,
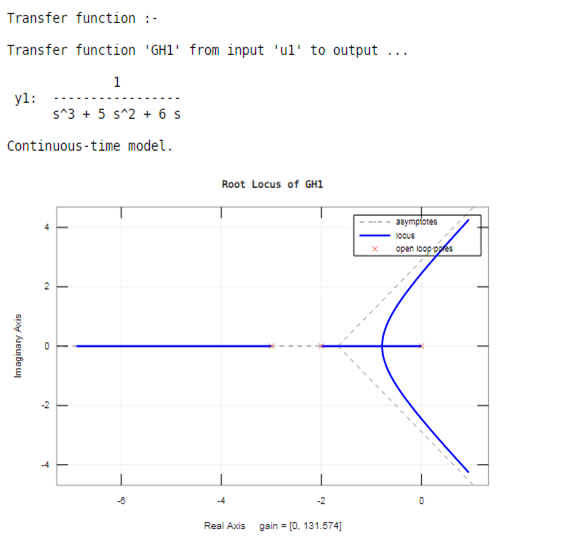
In this example, we can take the above transfer function for a root locus. We create the above transfer function on Matlab by using the tf inbuilt function. In tf function, we assign the coefficients of the above transfer function; in tf function, we take two square brackets, in first square brackets, we write the coefficients of numerator for the above transfer function (order s^4, s^3, ……, s, constant) and in second square brackets, we write coefficients of the denominator for above transfer function (order s^4, s^3……, s, constant). The comma separates these two square brackets. Then we use a rlocus function in brackets; we assign the variable which is use to generate a transfer function.
Code:
clc;
clear all;
close all;
disp ('Transfer function :- ');
GH1 = tf ( [ 1 ] , [ 1 5 6 0 ] )
rlocus (GH1)
Output:
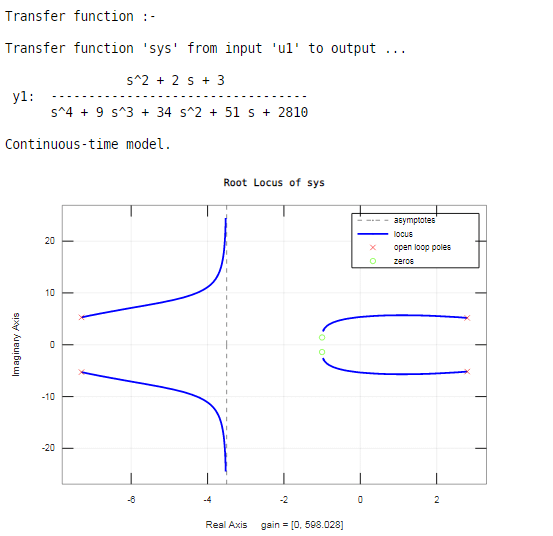
Example #3
Let us consider another one example,
Code:
clc;
clear all;
close all;
disp ('Transfer function :- ');
sys = tf ( [ 1 2 3 ] , [ 1 9 34 51 2810 ] )
rlocus(sys)
Output:
In this example, we have five poles and two zeros. The poles are shown by ‘×’, and the zeros are shown by ‘o’ on a root locus.
Root locus exists on the real axis between:
0 and -1
-2 and negative infinity
Recommended Articles
This is a guide to Root Locus Matlab. Here we discuss the basic concepts of root locus. And how we use a root locus in Matlab, what exactly syntax is used to create a root locus. In this article, we also saw some examples related to root locus with Matlab codes. You may also have a look at the following articles to learn more –